За най-малките (пък и не само за тях) – Компютрите през погледа на проф. Процесор Аритметиков

Шестнадесетичните числа

Миналия път се запознахме с двоичните числа, които са съставени само от две цифри – нула и едно. Десетичните числа пък са съставени от десет цифри – 0, 1, 2 и т.н. до 9. Десетичните числа се използват както в ежедневието, така и в сериозната математика. Двоичните числа, както видяхме в предишните материали, са удобни за използване в компютрите. И това е така, защото двете цифри 0 и 1 лесно се изразяват с физични състояния в хардуера.

Е, тогава, защо в компютрите се използват и така наречените шестнадесетични числа, които се състоят от 16 цифри. Една от причините за това е, че 16 = 2⁴, т.е. 16 е степен на двойката, а това прави преминаването от двоични в шестнадесетични числа и обратно много лесно. Освен това двоичните числа са трудни за различаване, защото се състоят само от единици и нули и защото записът им е прекалено дълъг. Например, ето две двоични числа, които отговарят на десетичните 101 и 103:

1100101 1100111

А паметта на компютъра или обемът на твърдия диск са много по-големи от 101 байта. Ето защо, въпреки че числата се представят в хардуера двоично, то компютърните специалисти боравят с шестнадесетични числа.

И така, какво представляват шестнадесетичните числа? За цифрите от 0 до 9 се използват същите символи, а вместо 10 се пише A, вместо 11 – B, и т.н. до F за 15. След това следва 10, защото се изчерпаха шестнадесетте цифри. Очевидно шестнадесетичното 10 ще е десетичното 16. Ето една таблица, която представя някои числа в трите бройни системи (и в този материал със запетайка ще разделяме всеки три цифри за прегледност, т.е. десетичният знак ще е точка, а запетайката е разделител на всеки три цифри).

десетично число	двоично число	шестнадесетично число
10	1,010	A
11	1,011	B
12	1,100	C
13	1,101	D
14	1,110	E
15	1,111	F
16	10,000	10
17	10,001	11
32	100,000	20

В миналия материал научихме как да преобразуваме двоични в десетични числа и обратно. Това превръщане за шестнадесетичните числа е аналогично:

(двоичното) 10,001 = 1 x 2⁴ + 0 x 2³ + 0 x 2² + 0 x 2¹ + 1 x 2⁰ = 16 + 1 = 17 (десетично)

(шестнадесетичното) 11 = 1 x 16¹ + 1 x 16⁰ = 16 + 1 = 17 (десетично)

Превръщането на десетични в шестнадесетични числа е по-трудно, но принципът е аналогичен на този за превръщането на десетични в двоични. Миналия път превърнахме 233 в двоично число. Ето как то се превръща в шестнадесетично.

Почваме със степените на 16: 16⁰ = 1, 16¹ = 16, 16² = 256. Последното число, 256, е по-голямо от 233, значи ще работим с 16¹ = 16. Изваждаме последователно 16-ци (т.е. изваждаме последователно 16¹) от 233, докато получим число по-малко от 16, което очевидно е остатък.

233 – 16 – 16 – 16 – 16 – 16 – 16 – 16 – 16 – 16 – 16 – 16 – 16 – 16 – 16 = 9

т.е. извадихме 14 пъти числото 16¹ от 233:

233 – 14 x 16¹ = 9

т.е. имаме (не забравяйте, че 14 = E):

233 = 14 x 16¹ + 9 x 16⁰ = Е x 16¹ + 9 x 16⁰

или

(десетичното) 233 = Е9 (шестнадесетично)

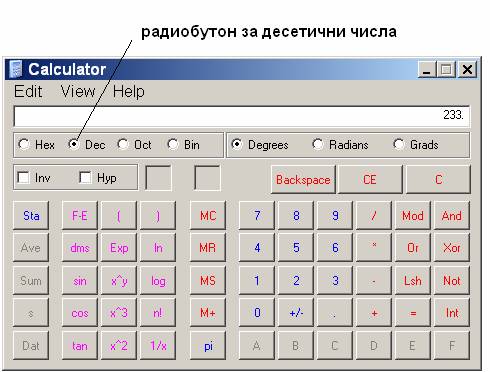
Същият резултат може да получите и с калкулатора на Windows. Стартираме калкулатора и написваме десетичното число като внимаваме радиобутона Dec да е включен.

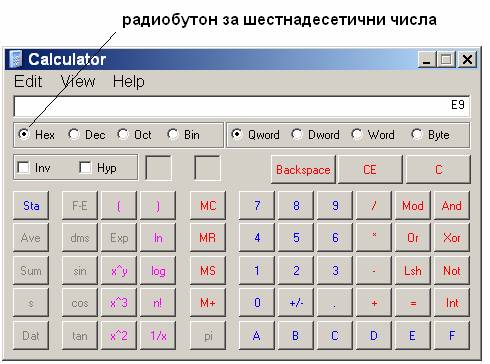
След което натискаме радиобутона Hex и получаваме E9.

Разбира се, че можем да се върнем обратно в десетично число. А това означава, че можем да напишем шестнадесетично число и да го превърнем в десетично. Забележете буквите A, B, C, D, E и F на последния ред на калкулатора – с тях се вкарват шестнадесетичните числа: те са активни само ако радиобутонът Hex е включен.

Споменахме, че много лесно се превръща от двоични в шестнадесетични числа и обратно. Именно това се използва от компютърните специалисти – те работят на практика с шестнадесетични числа, които в компютъра са представени като двоични числа. В следващата лекция ще разгледаме това превръщане, но тук само ще подскажем идеята, защото считаме, че вече имате достатъчно знания за да изведете правилото сами!

Разделяме двоичното число на четворки цифри. Знаем че десетичното 233 бе равно на двоичното 1110,1001. Е, лесно се вижда че първата четворка цифри е десетичното 14, което е шестнадесетичното E. Втората четворка цифри е 9. Т.е. числото е Е9. Помислете и за обратното превръщане – просто всяка цифра на шестнадесетичното число се изобразява като четворка цифри, които са двоично число:

E = 14 = 1110 и 9 = 9 = 1001,

т.е.

E9 = 1110,1001

Малко английски

И последно – в компютърните програми в повечето страни по Света се пише на английски. Затова нека видим как са на английски някои от думичките, с които се запознахте днес.

български	английски	произнасяне
шестнадесетичен	hexadecimal	хексадесимъл
бройна система	notation	нотейшън
превръщане	conversion	кънвършън
превръщане на десетични числа в двоични числа	the conversion of decimal numbers to binary numbers