Работа с матрици в програмата Excel

1. Матрици. Матрицата е правоъгълна таблица от числа. Тя представлява обобщение на понятието число и намира, подобно на векторите, изключително голямо приложение в науката. Обикновенно матриците се изписват с главни букви, A, B, C и т.н., а техните елементи се изписват с малки букви и се номерират с долни индекси, първият от които показва номерът на реда, а вторият – номерът на колоната.
 
 

Понякога е удобно размерностите на матриците да се изобразят като два долни индекса, които показват броят на редовете и колоните в матрицата. В този случай матрицата ще може да се отличава от даден неин елемент, например c_2,3, понеже е изписана с главна буква. А също така размерностите на матрицата се означават с големи букви (например A_M,N), докато индексите на елементите – с малки. Съгласно горесказаното трите матрици горе могат да се запишат като A_2,2, B_3,3 и C_2,3.

Матриците се събират и изваждат като се събират и изваждат съответните им елементи: за целта двете матрици трябва да са с еднакъв брой на редовете и еднакъв брой на колоните. Две матрици могат да се умножат само ако първата матрица има брой на колоните равен на брой на редовете на втората. Това лесно може да се съобрази (вместо да се запомня) от следния запис

C_K,L = A_K,M* B_M,L ,

където двете размерности в средата, трябва да са равни (в случая те са М) и съответно те “изчезват”,  като остават само тези в края. Съответната формула за елементите на резултантната матрицата е

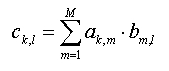
Образно представено това означава, че елемент в матрицата C, който стои на k-ти ред и l-та колона се получава чрез скаларното умножение на k-ти ред от матрицата A и l-та колона от матрицата B.

Матрица се умножава с число като всичките и елементи се умножават с това число. Ясно е, че получената матрица има същите размерности. Операцията делене на матрици, A/B, не може да се формулира еднозначно, понеже e възможно да съществуват много на брой матрици C, които умножени с B дават A или да не съществува нито една такава матрица C. Но ако B e правоъгълна матрица и има обратна матрица B^-1, то A*B^-1 и B^-1*A  са своего рода деление на матрици.

За всяка квадратна матрица A може да се изчисли нейната детерминанта, която се отбелязва с |A|. Ако  |A| # 0, то матрицата A има обратна матрица, която се отбелязва с A^-1. Произведенията A*A^-1 и A^-1*A дават единичната матрица, I, която има елементи единица на диагонала, а останалите са нули.

A*A^-1 = I и A^-1*A = I,

където

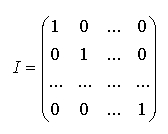
2. Събиране и изваждане на матрици в програмата Excel. Събирането и изваждането на матрици в Excel се извършва директно с използване на операциите на програмата. В таблицата (sheet) Addition файла matrices.xls са дадени две матрици A и B, с размерност три реда на две колони. Решаваме да разположим сумата на двете матрици в клетки F2:G4, затова в клетка F2 записваме формулата = B2 + B6. След натискане на клавиша Enter в клетката автоматично се изчислява сумата на елементите a_1,1 и b_1,1. След това разпъваме формулата надолу по колоната до клетка F4, а после разпъваме формулата до следващата колона G2:G4. Аналогичните действия извършваме, за да получим разликата на двете матрици. Резултатите могат да се видят във файла matrices.xls.

3. Умножение на матрици в програмата Excel. В същият файл, matrices.xls, в неговата таблица Multiplication са дадени две матрици A и B, с размерности, съответно 2x3 и 3x2, които са разположени в региони (клетки) B1:D2 и B5:C7. Решаваме да разположим матрицата C = A*B в клетки B10:C11, затова в клетка B10 написваме формулата =MMULT(B1:D2,B5:C7) и натискаме клавиша Enter. Избираме региона B10:C11 (в който ще се разполага матрицата C) и натискаме  клавиша F2, след което комбинацията от три клавиша (едновременно!) Ctrl-Shift-Enter. За упражнение получете матрицата D = B*A, която разположете в региона G10:I12.

4. Изчисляване на обратна матрица и детерминанта в програмата Excel. В същият файл, matrices.xls, в неговата таблица Inverse са дадени две матрици A и B, и C = A*B. Обратната матрицата C^-1 ще разположим в клетки B15:C16. Затова написваме формулата =MINVERSE(B10:C11) в клетка B15 и натискаме клавиша Enter. Избираме региона B15:C16 (в който ще се разполага матрицата C^-1) и натискаме  клавиша F2, след което комбинацията от три клавиша (едновременно!) Ctrl-Shift-Enter. За упражнение намерете обратната матрица на D, която разположете в региона B19:D21. Детерминантата на C е намерена в клетка F16, в която е написана формулата = MDETERM(B10:C11). За упражнение намерете детерминантите на C^-1, D и D^-1. Забележете, че първата детерминанта е 1/|C|, а последните две детерминанти са нула.

Автор: Пламен Пенчев, Ph.D.
Авторски права: Материалът или част от него могат да се използват свободно (копирани на друг сайт) в обучението на български или македонски студенти само ако в сайта изрично се цитира тази оригинална статия във вида: П.Пенчев, Работа с матрици в програмата Excel, Списание "Коснос" (www.kosnos.com), брой 4, 2007 г.