В този материал ще представим едно извеждане на няколко тригонометрични формули с цел, не по-лесното им запомняне, а разбиране на същността на тези отношения.

1. cos(j₁ - j₂)

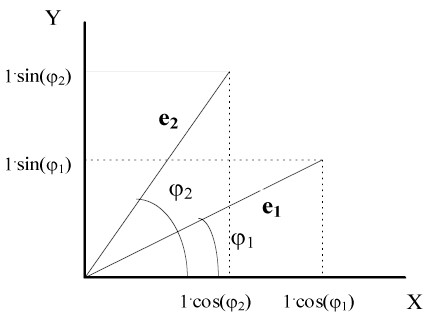
Да разгледаме два единични вектора e₁ и e₂ в равнината (X, Y), които сключват ъгли с оста X, съответно равни на j₁ и j₂. Тогава ъгълът между тях е j₂ - j₁. На фигура 1 са дадени декартовите координати на векторите, както и ъглите между тях и абцисата. Понеже векторите са единични, то техните координати в равнината (X, Y) са равни на 1^.cos(j₁) и 1^.sin(j₁) за първия вектор, и 1^.cos(j₂) и 1^.sin(j₂) за втория вектор.

2. cos(j₁ + j₂) :

Понеже sin(x) е нечетна функция, а cos(x) - четна функция, при заместване на j₂ с  -j₂ в равенство (1) получаваме:
 

Използваме равенство (2) и отношенията cos(j + p/2) = -sin(j) и sin(j + p/2) = cos(j):

4. sin(j₁ - j₂):

Използваме равенство (3) и факта, че sin(x) е нечетна, а cos(x) - четна функция, т.е. sin(-j) = -sin(j) и cos(-j) = cos(j):
 

5. cosj₁cosj₂

Ако съберем равенства (1) и (2) получаваме:

cos(j₁ - j₂) + cos(j₁ + j₂) =
[cosj₁cosj₂ + sinj₁sinj₂] + [cosj₁cosj₂ - sinj₁ sinj₂] =
= 2cosj₁cosj₂

т.е.
cosj₁cosj₂ = [cos(j₁ - j₂) + cos(j₁ + j₂)] / 2      (5)
 

cos(j₁ - j₂) - cos(j₁ + j₂) =
= [cosj₁cosj₂ + sinj₁sinj₂] - [cosj₁cosj₂ - sinj₁ sinj₂] =
= 2 sinj₁sinj₂

т.е.
 
sinj₁sinj₂ = [cos(j₁ - j₂) - cos(j₁ + j₂)] / 2      (6)
 

sin(j₁ + j₂) + sin(j₁ - j₂) =
= [sinj₁cosj₂ + cosj₁ sinj₂] + [sinj₁cosj₂ - cosj₁sinj₂] =
= 2 sinj₁cosj₂

т.е.
sinj₁ cosj₂  = [ sin(j₁ + j₂) + sin(j₁ - j₂) ] / 2                             (6)