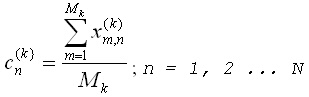
Идеята на този метод е изключително елементарна [1] – изчислява се разстоянието в пространството на образите между класифицирания образ и центроидите на класовете. Образът се избира от този клас, до чийто центроид има най-малко разстояние от образа. Координатите (признаците), cn, на k-тия центроид се изчисляват по следния начин:
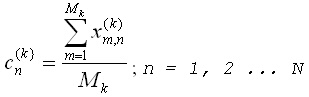
където с k е означен k-тият клас, с m – m-тият обект от този клас, Mk е съответният брой образи в този клас, n e номерът на признака, а N e броят признаци (размерността на образите).
Видът на разстоянието, което се използва, се избира от изследователя и обикновено зависи от типа на признаците, които съставят хемометричните образи. Оптималната за дадена класификация мярка за разстояние зависи и от типа на хемометричните обекти, чийто образи се класифицират – ето защо е правилно да се проверят няколко мярки с помощта на обучаваща и тестваща извадка. Обучаващата извадка се използва да се изчислят центроидите на класовете, а образите от тестващата извадка се използват като непознати образи, чиято класификация се оптимизира.
На фигура 1 е показана класификацията по два класа на два “непознати” образа, X1 и X2 в двумерното пространство: на фигурата са изобразени съответните Евклидови разстояния. Признаците на образите представляват абсорбцията на най-интензивната ивица в ИЧ спектр, съответно, в интервалите 1079-1003 cm-1 (x1) и 3578-3278 cm-1 (x2). В първия клас са съединения, които са първични алкохоли (кръговете), а в нулевия клас – които не са първични алкохоли (квадратите). Съответните им центроиди са изобразени като ромб (за клас 1) и триъгълник (за клас 0), а двата “непознати” образа са изобразени като празен квадрат (X1) и празен кръг (X2).
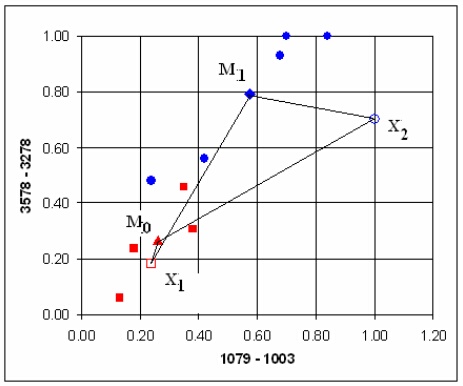
Фигура 1. Класификация по разстоянието до центроидите. Обучаващата извадка се състои от девет образа, съответно 4 от клас 0 и 5 от клас 1.
От фигурата се вижда, че образ X1 е по-близо до центроида на нулевия клас, а X2 – до центроида на първи клас. В таблица 1 са дадени съответните образи от фигура 1.
Таблица 1. Хемометричните обекти и образи, които са изобразени на фигура 1.
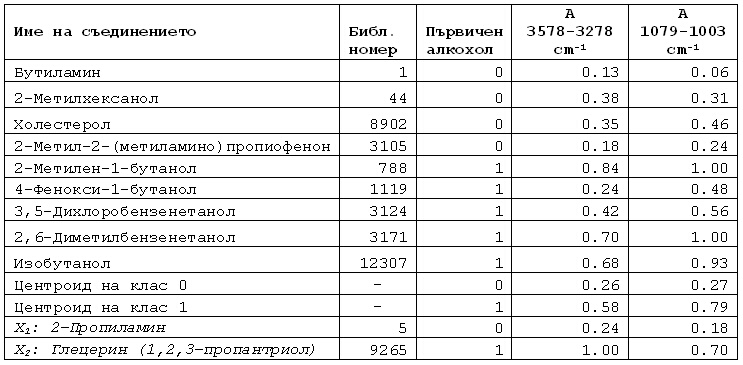
Интересно е да се отбележи, че образ 6 от обучаващата извадка, 4-Фенокси-1-бутанол, е по-близо до центроида на нулевия клас, въпреки че образът е от първи клас.
Приведеният пример бе нарочно избран да е в двумерното пространство, за да може да се визуализира концепцията на метода., но на практика класификацията обикновено се провежда в многомерното пространство, с размерност N > 3. В този случай визуализирането на разстоянията до центроидите е невъзможно и решение се взима чрез сравняване на разстоянията.
Очевидно е, че методът позволява класифицирането да се извърши спрямо повече от два класа - просто се изчисляват повече от две разстояния и те се сравняват. На практика
Ако класовете са само два, то класифициращият критерий (decision criterion) за непознатия образ X, y(X), може да се запише по следния начин:
y(X) = 1/2[d(X, C1)2 – d(X, C2)2]
където с d(X, Ck) са означени съответните разстояния от X до двата центроида C1 и C2.
Очевидно, че ако y(X) < 0, то X е от клас 1, ако y(X) > 0, то X е от клас 2, и ако y(X) = 0, то не може да се вземе решение.
Ако се използва Евклидово разстояние, то класифициращият критерий е равен на:
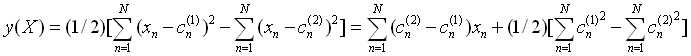
Ако групираме първата разлика и втората разлика, то критерият е равен на
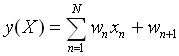 (1)
(1)
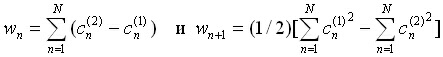 (2)
(2)
Уравнение (1) представлява скаларно произведение между образ, чийто първи N координати са равни на координатите на класифицирания образ и последната му координата е единица, с тегловен вектор W, чийто координати са дадени с уравнение (2). Както бе дефинирано по-горе, ако това скаларно произведение е отрицателно, то образът е от клас 1, а ако е положително - от клас 2. На уравнения (1) и (2) ще се спрем отново в следващия материал, който разглежда линейната обучаваща машина. Засега само ще споменем, че в пространството на оригиналния образ (т.е. с размерност N, а не N+1), класифициращата повърхност е една хиперравнина (т.е. N мерна равнина), която минава през центъра на отсечката, която свързва двата центроида и е перпендикулярна на нея. Това ясно е илюстрирано на фигура 2, която представя същите образите от фигура 1, и съответно от таблица 1: в двумерното пространство класифициращата хиперравнина е всъщност права, а в тримерното тя ще представлява равнина.
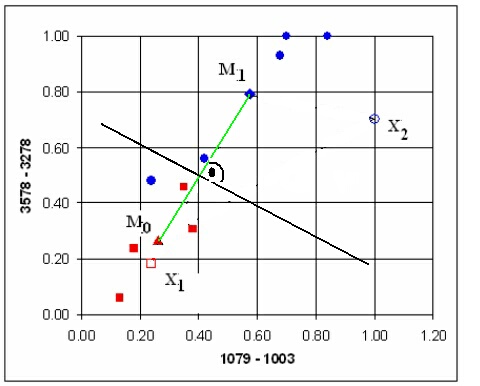
Фигура 2. Класификация по разстоянието до центроидите. Зелената отсечка свързва двата центроида M1 и M2, а черната права, която минава през центъра на отсечката, е класифициращата хиперравнина, която всъщност е права в двумерното пространство.
[1] K. Varmuza; Chemometrics. Springer
Verlag, Berlin, 1980.
..
Автор: Пламен
Пенчев, Ph.D.
[ това е материал от брой 16 на списание "Коснос" www.kosnos.com ]