
Електромагнитното лъчение от инфрачервената област на спектъра се използува за изследване на промени в молекулната конфигурация. Основа за това е фактът, че енергията на инфрачервеното лъчение е от същия порядък, както разликата в енергиите на вибрационните енергетични нива в молекулатан а химичните съединения. Методът, използуван за изследване на молекулни трептениия на базата на абсорбция на инфрачервено лъчение, се нарича инфрачервена спектроскопия. Един друг, принципно различен метод за изследване на вибрацията на атомите в молекулите, е Раман-спектроскопията. При него се използува нееластичното разсейване на монохроматично лъчение, чиято честота се комбинира със собствените честоти на трептене на атомите в молекулите.Вибрационна спектроскопия
Инфрачервената област от електромагнитния спектър се разделя традиционно на подобласти: близка, средна и далечна - вижте фигура 1.

Честотите на ивиците, съответствуващи на основните трептения на атомите в молекулите на органичните съединения, са разположени в средната инфрачервена област (4000-400 см-1), поради което ние ще съсредоточим вниманието си по-подробно върху нея. В далечната инфрачервена област се изследват трептенията на атомите в неорганичните вещества, на някои връзки в комплексните съединения и на вибрации в кристалната решетка. От разглежданията в предходната глава видяхме, че в тази област са разположени и някои абсорбционни ивици на ротационни преходи. В близката инфрачервена област се проявяват ивиците на повечето обертонови и съставни честоти, както и на някои важни електронни преходи. Необходимостта от разграничаване на тези преходи (както и някои технически особености на приемниците), наложиха напоследък да бъде предложено близката инфрачервена област да бъде разделена на две: (1) близка (същинска) включваща интервала 8333-4000 см-1, в която се проявяват обертоновите и съставни ивици на спектрите; (2) Хершел-ИЧ (H-IR), влючваща интервала 13333-8333 см-1 т.е. 750-1200 nm, в която се наблюдават спектри, съдържащи ивици на обертонове и комбинация от основни трептения и електронни преходи.
1. Трептене на двуатомна молекула. Хармоничен осцилатор. Атомите, изграждащи молекулите, се намират в непрекъснато движение. При трептене на една двуатомна молекула става периодично свиване и разтегляне на химичната връзка спрямо равновесното положение на атомите. Тази промяна на междуатомното разстояние е свързана с изменение на силата на взаимодействие между ядрата, която от своя страна е функция на енергията на валентните електрони. Следователно вибрационната енергията на една двуатомна молекула, намираща се в дадено електронно състояние, ще зависи от междуядреното разстояние r.
Дължините на химичните връзки в двуатомните молекули са много по-големи от отклоненията на трептящите атоми спрямо равновесното им положение. Ето защо при изучаване зависимостта на енергията на двуатомните молекули от периодичната промяна на междуядреното разстояние, тези молекули могат с известно приближение да се разглеждат като хармонични осцилатори.
2. Класическо разглеждане на хармоничния осцилатор. Двуатомната молекула може да бъде представлява като две маси, m1 и m2, свързани с еластична връзка на разстояние r0 - фигура 2.
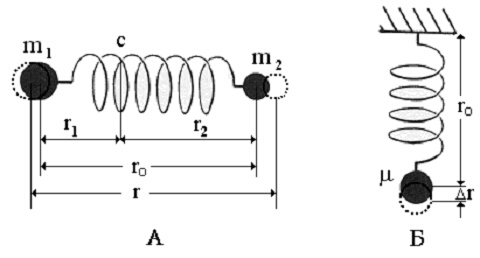
Фигура 2. Модел на двуатомна молекула (А) и на хармоничен осцилатор (Б), когато задачата от две тела е приведена до задача за едно тяло с приведена маса m.
Ако телата бъдат отклонени, например на разстояние r и се оставят свободни, те започват да трептят около равновесното положение под влияние на възвръщащата сила F. За случаите, при които отклонението от равновесното положение Dr = r - r0 e малко в сравнение с дължината r0, e в сила законът на Хук, според който възвръщащата сила е пропорционална на деформацията:
F = -k(r-r0) = -k Dr (1)
Знакът минус в (1) показва, че възвръщащата сила има посока, обратна на деформацията, а kсъответствува на силата, възникваща при единица отклонение.
Съгласно втория принцип на динамиката, движението на телата се дава с изразите:
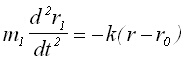 (2)
(2)
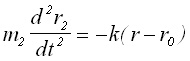 (3)
(3)
Използувайки отношенията от уравнения (2.1) и (2.4) се получава:
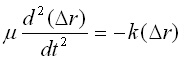 или
или 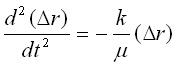 (4)
(4)
където m се нарича приведена маса (reduced mass) и се изразява по следния начин - m = m1m2/(m1 + m2); има още един запис на това равенство: 1/m = 1/m1 + 1/m2.
Оказва се, че движението на двата атома в разглеждания модел се свежда до трептене на материална точка с маса m, равна на приведената маса, т.е. до трептене на харамоничен осцилатор - вижте фигура 2 Б.
Диференциално уравнение (4) има решение от вида:
Dr = Acos(wt+j) (5)
където: А е амплитуда на трептенето, w - кръгова честота и j - фазова константа.
Заместването на (5) в (4) води до уравнението:
-Aw2cos(wt+j)= -A(k/m)cos(wt+j) (6)
което се удовлетворява при условие, че:
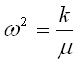 или
или 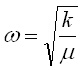 (7)
(7)
Уравнението Asin(wt+j) също е решение на (4), но удовлетворява друго начално условие.
Тъй като кръговата честота w = 2pn, то за честотата на трептене на хармоничния осцилатор ?? получава:
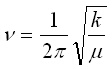 [Hz] или
[Hz] или 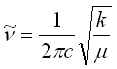 [cm-1] (9)
[cm-1] (9)
В резултат на тези разглеждания идваме до извода, че хармоничният осцилатор притежава само една, определена честота на трептене, която зависи от приведената маса m и коефициента k, който от своя страна е функция от свойствата на еластичната връзка. От този израз, обаче, не става ясно какви стойности може да приеме амплитудата, а следователно и енергията на трептене.
Ако реалните двуатомни молекули са хармонични осцилатори, те трябва да притежават само една честота на трептене, определена по уравнение (9). Опитните данни показват, че (9) описва с добро приближение наблюдаваните честоти, при което константата k характеризира здравината на химичната връзка; тя се нарича силова константа.
Зависимостта на потенциалната енергия на двуатомните молекули U от междуядреното разстоние r е сложна крива с минимум при равновестното разстояние r0 - вижте фигура 3.
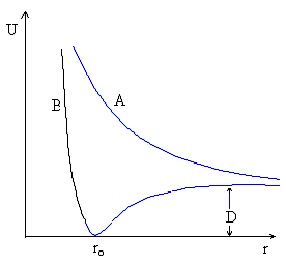
За случая на трептения, при които отклоненията Dr от r0 са малки, U(r) може да се разложи в ред в близката околност на r0:
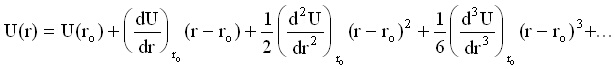 (10)
(10)
В уравнение (10) U(r0) може да се приеме за нула, а (dU/dr)r0 =0. За случая на малки отклонения, членовете на реда по-високи от втора степен магат да се пренебрегнат. Тогава приемайки (d2U/dr2)r0 =k се получава:
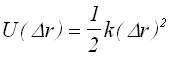 (11)
(11)
От (11) следва,че потенциалната крива на хармоничен осцилатор, може да се представи като парабола.
3. Квантово-химично разглеждане на хармоничния осцилатор. Молекулите като микросистеми се подчиняват на квантовомеханичните закони. При решаване на уравнението на Шрьодингер за хармоничния осцилатор:
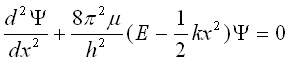 (12)
(12)
(x
= Dr)
се установява, че енергията може да приема стойности, удоволетворяващи
уравнението:
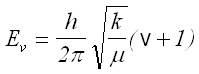 (13)
(13)
където v е вибрационно квантово число, което може да заема всички цели неотрицателни стойности: v = 0,1,2,...
Замествайки (9) в (13), за енергията на трептене на хармоничния осцилатор получаваме окончателно:
![]() [J] (14)
[J] (14)
Следователно квантовохимичните разглеждания водят до принципно различин резултат: енергията на хармоничния осцилатор може да заема само определени стойности, давани с уравнение (14).
За вибрационните термове G(v) се получава:
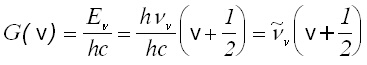 [cm-1] (15)
[cm-1] (15)
Ако на v се дават последователно разрешените стойности 0,1, 2..., за вибрационната енергия Еv (Е0 е т.н. нулева вибрационна енергия):
при v
= 0 се получава Е0
=
1/2 hn;
при v
= 1 се получава Е1
=
3/2 hn;
при v
= 2 се получава Е2
=
5/2 hn.
Следователно според квантовата механика
хармоничният осцилатор притежава система от равноотстоящи енергетични нива
- вижте фигура 4.
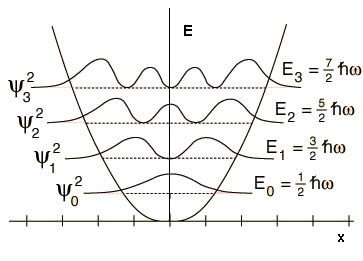
Разликата между кои да са две стационарни състояния DЕv, например първо и нулево е:
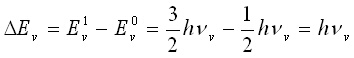 (16)
(16)
За да се осъществи преход между тези две енергетични състояния, молекулата трябва да погълне квант енергия Екв.
Екв = hnкв (17)
Следователно при преход между две съседни стационарни вибрационни състояния се поглъща електромагнитно лъчение с честота, равна на собствената механична честота на трептене на атомите в молекулата.
Квантовомеханичните разглеждания водят до следното подборно правило за хармоничния осцилатор: разрешени са само преходи между съседни вибрационни състояния, т.е.
Dv = +1 или Dv = -1
От последното следва, че спектърът на хармоничния осцилатор се състои от една единствена ивица, т.е. квантовомеханичните разглеждания водят до същия резултат, както класическите.
Въз основа на изложеното се идва до заключението, че ако двуатомните молекули представляват хармонични осцилатори, те би трябвало да имат само една абсорбционна ивица. Това противоречи на експерименталните данни; в инфрачервените спектри на двуатомните молекули се наблюдават повече абсорбционни ивици.
Литература
Автор: Проф. дхн Георги Андреев