Степени и логаритми

(вижте другите учебни материали)

Това е материал за студенти физици или химици. Авторът на материала многократно се е сблъсквал с безпомощността на студентите в дисциплината "Инструментални методи за анализ", където се борави със степени и логаритми, и затова счита, че този материал ще е полезен за тях.

1. Степени. До понятието степен се стига след обобщаване на операцията умножение. Например ако числото a го умножим n пъти, това се означава така:

aaa...a = aⁿ

Съвсем логично се получава, че

aⁿ a^m = (aaa...a)(aa...a) = a^n+m

За да няма противоречие, ако числото 1 го разделим m пъти на числото a това се записва по следния начин:

1/(aaa...a) = 1 / a^m = a^-m

А последното равенство води до

aⁿ / a^m = (aaa...a)/(aa...a) = aⁿ a^-m = a^n-m

Когато n и m са цели числа няма проблеми да си представим действията със техните степени, но какво ще се получи ако те не са цели числа, а реални числа? Отново важат написаните равенства, но има едно основно изискване за основата на степента и то е че тя трябва да е положително число, т.е. a > 0.

Ако е изпълнено a > 0 то за всеки какви да е реални числа b и c е изпълнено (при умножение степените се събират):

a^b a^c = a^b+c

Както и че при делене степените се изваждат:

a^b / a^c = a^b-c

Ако двете степени са равни, то от горното равенство се получава, че всяко положително число на нулева степен е равно на единица:

a^b / a^b = 1 = a^b-b = a⁰

т.е.

a⁰ = 1

Аналогично се дефинира и отрицателна степен:

1 / a^b = a⁰ / a^b = a^0-b = a^-b

т.е.

1 / a^b = a^-b

Ако имаме степенно уравнение, в което основата на степента е неизвестна,

x^b  = c,

то уравнението се решава по следния начин:

x = c^1/b

В този случай, ако b е цяло число решението, c^1/b, се нарича корен бе-ти от це. При b = 2 се получава познатият ни корен квадратен, а при b = 3 - корен кубичен.

Уравнението

a^x  = c,

не се решава с коренуване, а с логаритми - вижте следващата точка.

2. Логаритми. Дефиницията на логаритъм, log_ab, е следната красива формула (чете се "логаритъм а-ти от бе" или "логаритъм от бе при основа а"):

a^loga^b = b

Така написана формулата означава, "Логаритъм е това число, на което трябва да повдигнем основата, за да получим логаритмуваното число!". Например десетичен логаритъм от 100 е 2,

log₁₀100 = 2,

тъй като

10² = 10^(log10¹⁰⁰⁾ = 100

По същия начин log₁₀10 = 1 и log₁₀1 = 0, тъй като

10¹ = 10^(log10¹⁰⁾ = 10  и   10⁰ = 10^(log10¹⁾ = 1

На практика лявата част на дефиниционната формула, a^loga^b, означава антилогаритмуване на логаритъм, т.е. изпълнение на обратната операция върху операцията логаритмуване, което неминуемо води до непроменен операнд b.

Останалите свойства на логаритмите лесно може да се изведат от тяхната дефиниционна формула. Необходимо е равенството, което трябва да докажем, да го положим в степените, защото

a^b = a^c Ю b = c при a > 0

И обратно, при a > 0

b = c Ю a^b = a^c

Например, следното свойство

log_ab + log_ac = log_abc

следва от следното равенство

a^(loga^b+loga^c) = a^loga^b a^loga^c = bc = a^loga^bc

По същия начин, следното свойство

log_ab - log_ac = log_ab/c

следва от следното равенство

a^(loga^b-loga^c) = a^loga^b / a^loga^c = b/c = a^loga^b/c

Ключовото равенство

log_ab^c = c log_ab

следва от (с ^{b^c} сме означили b^c)

a^(loga^{b^c)} = b^c = (a^loga^b)^^c = a^{(c log}a^b)

Тук с ^ означихме вдигане на степен, защото хипертекстът е ограничен само с едно ниво на горните индекси.

Частен случай на горната формула е log_aa^c = c log_aa = c, което може да се интерпретира отново като прилагане на логаритмуването като обратна операция на степенуването.

Следната формула, която лесно се помни понеже двете бе-та са едно до друго, се извежда отново с дефиниционната формула на логаритмите:

log_ab log_bc = log_ac

a^(loga^{b log}b^c) = (a^log_ab)^loga^c = b^logb^c = c = a^loga^c

Тук с ^ отново означихме вдигане на степен, защото хипертекста е ограничен само с едно ниво на индексите.

Аналогично от горното уравнение следва зависимостта

log_bc = log_ac / log_ab

Последната зависимост се използва много често за изчисляване на десетичен логаритъм или привеждане на формули, съдържащи натурален логаритъм във формули, съдържащи десетичен логаритъм. Така за десетичен логаритъм се получава

lg c = log₁₀c = log_ec / log_e10 = ln c / ln 10 = ln c / 2.30

или

lg c = ln c / 2.30

или

ln c = 2.30 x log₁₀c

Например уравнението на Нернст (Nernst equation) за електродния полу-потенциал на двойка редуктор-окислител с активности a_Red и a_Ox

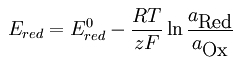
се привежда в уравнението

(вижте другите учебни материали)

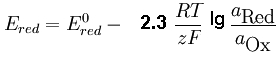
Автор: Пламен Пенчев, Ph.D.

[ това е материал от брой 21 от юли 2008 г. на списание "Коснос"www.kosnos.com ]