Случайна Величина
Химията е наука, която се занимава с преобразуването
и строежа на веществото. Основни понятия в химията са химичните и физикохимичните
величини, чието измерване е една от главните задачи на химичния експеримент.
Понятието величина е удобна научна фикция, служеща успешно в практиката
на човека, въпреки че в абсолютен смисъл величината няма стойност. Едно
по-точно измерване на концентрацията на даден хомогенен разтвор би показало,
че тя се изменя по място и по време, вследствие на случайните флуктуации
на разтвореното вещество. Аналогично, масата на определено количество вещество
се променя непрекъснато от влагата и от изпарението на веществото. Но като
понятие величината предполага една стойност, наречена истинска стойност
на величината, която експериментаторът се стреми да определи. В неговите
възможности е само оценка на тази стойност посредством набор
от опитни стойности и то приближена оценка, която той дава
с определена вероятност за нейната истинност.
1. Представа за случайна величина. Опитът
показва, че при повтаряне на дадено измерване, се получават стойности на
величината, които могат да се различават една от друга, независимо от постоянството
на експерименталните условия. Тези стойности не могат да се предскажат
преди опита. Това са така наречените случайни величини. За разлика от тях,
неслучайните величини имат точно определена стойност, която може да се
предскаже преди опита или получаваните в резултат на измерванията стойности
са равни една на друга. Различават се дискретни и непрекъснати
случайни величини. Когато възможните значения на една случайна величина
са краен или изброимо безкраен
брой, тя е дискретна. В повечето случаи при химичните измервания стойностите
на случайната величина могат да се разполагат в даден интервал, като заемат
коя да е реална числена стойност в него (например концентрацията на едно
вещество е в интервала 0 - 100%). Това са така наречените непрекъснати
случайни величини.
При измерването на дадена величина се забелязва,
че получените стойности (случайни величини) са групирани по определен начин
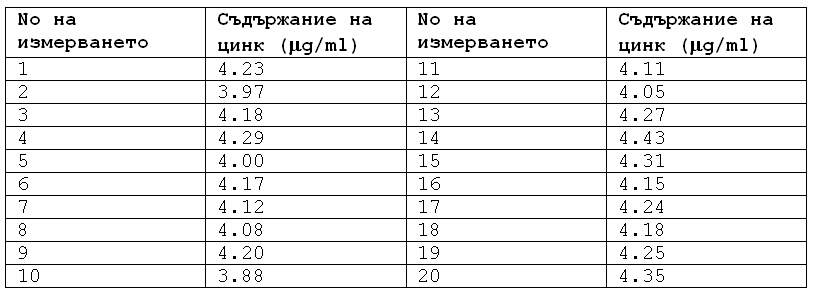
около дадена стойност. В таблица 1.1 са представени резултатите от двадесет
измервания на съдържанието на цинк в питейна вода.
Таблица 1.1. Съдържание на цинк
в питейна вода.
 .
.
За да се добие представа за характера
на получаваните случайни величини, може да се извърши следното: най-малката
стойност е 3.88, а най-голямата е 4.43, т.е. всички стойности са в интервала
(3.85, 4.45). Този интервал се разделя на шест интервала с дължина
на всеки равна на 0.10 и се построява хистограмата, показана на фигура
1.1. Височината на всеки от правоъгълниците е равна на броя на резултатите,
намиращи се в съответния интервал, включително и тези равни на дясната
граница на интервала.
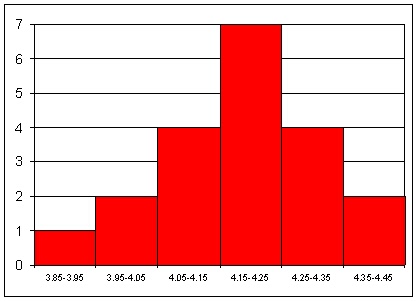
Фигура 1.1. Хистограма на
резултатите от таблица 1.1 |
... |
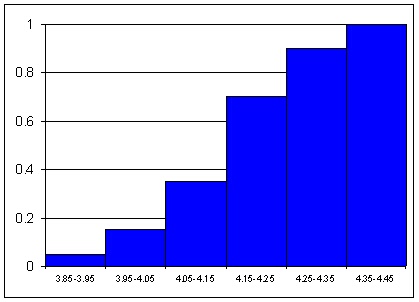
Фигура 1.2. Емпирична функция на
разпределение на резултатите от таблица 1.1 |
Прави впечатление, че в интервала (4.15,
4.25), който е разположен почти в средата, има най-много стойности (седем)
и че с отдалечаване от него на другите интервали в тях намалява броят на
експерименталните стойности. Това е обща закономерност на получаваните
резултати при почти всички използувани методи за измерване. Същата хистограма
е по-правилно да се построи, като височината на стълбовете се нормира,
т.е. се раздели на общия брой резултати. Така получените числа 1/20, 2/20,
4/20, 7/20, 4/20 и 2/20 се наричат относителни честоти на поява на
случайните величини в съответните интервали. Може да се построи
и друга хистограма, в която височината на даден стълб, се определя като
сума от височините на всички стълбове, разположени в ляво от дясната граница
на съответния интервал. На фигура 1.2 е представена тази хистограма, като
височините на стълбовете са нормирани, т.е. сумирани са нормираните височини
от хистограмата на фигура 1.1. Втората хистограма показва честота
на появата на случайна величина по-малка от дадено число (дясната граница
на интервала) и се нарича емпирична функция на разпределение на случайната
величина. При увеличаване на броя на измерванията относителните
честоти, както на първата хистограма, така и на втората, се стабилизират,
което означава, че при провеждане на все по-голям брой опити те клонят
във вероятностен смисъл към определени числа, наречени вероятности.
Практически това означава, че при нарастване на броя на измерванията и
намаляване на големината на интервалите горните части на хистограмите от
фигури 1.1 и 1.2 клонят към определени криви. Хистограмата от фигура 1.1
(ако се нормира и представлява относителните честоти на поява на случайната
величина) клони към крива, наречена плътност на разпределение на
случайната величина, а тази от фигура 1.2 към функция на
разпределение на случайната величина. Функцията на разпределение
напълно характеризира случайната величина: тя показва
каква е вероятността случайната величина да бъде по-малка от дадена стойност.
За непрекъснатите случайни величини тя е нарастваща, непрекъсната и диференцируема
функция и нейната първа производна е плътността на разпределение.
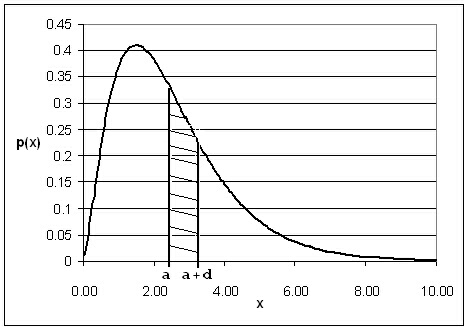
Фигура 1.3. Плътност на разпределение
p(x)
на произволна случайна величина x.
На фигура 1.3 е показана примерна крива
на плътност на разпределение у
= р(х). Тя е неотрицателна функция.
Защрихованата площ между правите х
= а и х
= а + d е вероятността случайната
величина да заема стойности между а
и а + d
и при малък интервал d
тя може да се апроксимира с площта на правоъгълник с ширина d
и височина р(a).
Вероятността случайната величина X
да е в произволен интервал (а,b)
се дава с интеграла
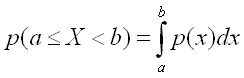
Вероятността случайната величина да е в
интервала ( -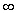 ,+
,+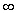 )
е единица и затова плътността на разпределение трябва да е нормирана (т.е.
умножена с подходяща константа), така че
)
е единица и затова плътността на разпределение трябва да е нормирана (т.е.
умножена с подходяща константа), така че
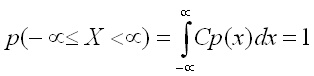
Функцията на разпределение на непрекъсната
случайна величина се дава с интеграла:
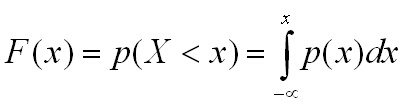
Дискретната случайна величина може напълно
да се зададе със своя вероятностен ред, който е подобен на плътността на
разпределение и който дава вероятностите за получаване на съответните стойности.
Таблица 1.2 показва вероятностния ред на случайната величина "сума от точките
на две хвърлени зарчета".
Таблица 1.2. Вероятностен ред на
случайната величина "сума от точките на две хвърлени зарчета". Xk
- стойност на случайната величина, pk
- вероятност за нейното заемане.

Функцията на разпределение на същата случайна
величина може да се даде таблично. По аналогия с тази на непрекъснатата,
тя се получава по формулата:
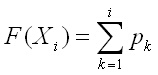
Тя е представена в таблица 1.3 и числата
от долния ред показват вероятностите случайните величини да заемат стойности
по-малки или равни от стойностите в горния ред.
Таблица 1.3. Функция на разпределение
на случайната величина "сума от точките на две хвърлени зарчета". Xk
- стойности на дискретната случайна величина; F(Xk)
- нейната функция на разпределение.

Данните от таблици 1.2 и 1.3 са изобразени
на фигури 1.4. и 1.5.
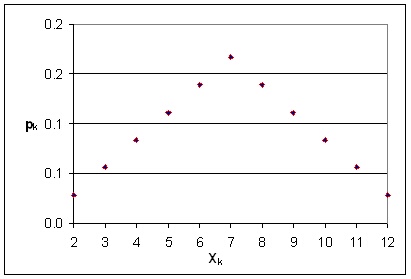
Фигура 1.4. Плътност на разпределение
на дискретната случайна величина таблица 1.2. |
... |
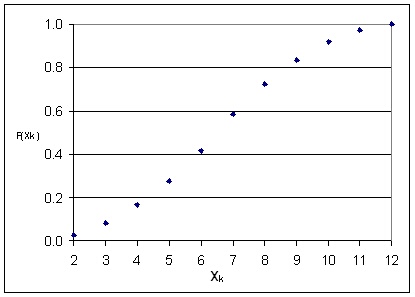
Фигура 1.5 Функция на разпределение
на случайната величина от таблица 1.2. |
2. Числови характеристики на случайните
величини. Функцията на разпределение напълно характеризира случайната
величина, но в повечето случаи не е нужен нейният вид. Достатъчно е да
се даде оценка за стойността на измерваната величина и да се посочи с определена
вероятност интервалът, в който тя се намира. Поради тези причини важна
роля играят две числови характеристики на разпределението на случайната
величина: математическото очакване и дисперсията.
Математическо очакване на дискретна
случайна величина се дефинира като сумата:
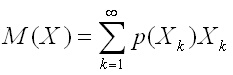 (1.1)
(1.1)
а за непрекъсната случайна величина
чрез интеграла:
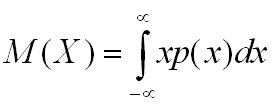 (1.2)
(1.2)
Дисперсията на случайна величина се дефинира
като математическо очакване от квадрата на разликата между случайната величина
и нейното математическо очакване.
D(Х) = М[Х - М(Х)]2
Или използвайки формули (1.1) и (1.2) получаваме:
- за дискретна случайна величина
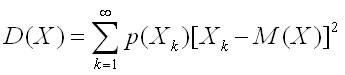
за непрекъсната случайна величина
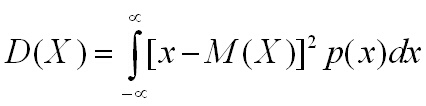 Обърнете внимание, че М(Х)
и D(Х)
са числа, а не някакви функции. Те просто се означават със скоби, за да
се покаже на коя случайна величина са числови характеристики, така както
е направено по-долу при седемте свойства.
Обърнете внимание, че М(Х)
и D(Х)
са числа, а не някакви функции. Те просто се означават със скоби, за да
се покаже на коя случайна величина са числови характеристики, така както
е направено по-долу при седемте свойства.
Плътността на вероятността р(Х),
съответно вероятностите р(Хк),
са неотрицателни величини и поради това дисперсията е неотрицателно число.
Математическото очакване може да бъде, както положително, така и отрицателно
число. Неговата стойност, както се вижда от (1.1) и (1.2), се определя
в най-голяма степен от най-вероятните стойности. Физическият смисъл на
дисперсията е, че тя е мярка за разсейването на случайните величини около
математическото очакване.
3. Свойства на числови характеристики
на случайните величини. Математическото очакване и дисперсията са числа,
които характеризират дадена случайна величина. Сумата, разликата, произведението
и частното от случайни величи е отново случайна величина. За някои от тези
действия могат да се изведат зависимости между числените характеристики
на резултантната случайна величина и тези на оригиналните. Тези зависимости,
дадени по-долу, не са аксиоми, а могат да се изведат от дефиницията на
математическото очакване и дисперсията (вижте задачи 1 - 5 и тяхното
решение).
Математическото очакване и дисперсия имат
следните свойства:
1. Математическото очакване на неслучайна
величина (константа) е равно на неслучайната величина (нейната единствена
стойност).
М(С) = С
2. Неслучайната величина (константа) може
да се изнася извън знака на математическото очакване.
М(СХ) = СМ(Х)
3. Математическото очакване на сума
от случайни величини е равно на сума от математическите им очаквания.
М(Х + У + ... + Z) = М(Х) + М(У)
+ ... + М(Z)
3a. Прилагайки това свойство и предишното
получаваме
M(Х - Y) = M[Х + (-1)Y] = M(Х) +
M[(-1)Y] = M(Х) + (-1)M(Y) = М(Х) - М(Y),
т.е.
M(Х - Y) = М(Х) - М(Y),
4. Математическото очакване на произведение
на независими случайни величини е равно на произведение на
математическите им очаквания.
М(ХУZ) = М(Х)М(У)М(Z)
5. Дисперсията на неслучайна величина (константа)
е нула.
D(С) = 0
6. Неслучайната величина може да се изнася
извън знака на дисперсията. Изнесената неслучайна величина се повдига на
квадрат.
D(СХ) = С2D(Х)
7. Дисперсията на сума от независими
случайни величини е равна на сума от техните дисперсии.
D(Х + У + ... + Z) = D(Х) + D(У)
+ ... + D(Z)
7a. Прилагайки това свойство и предишното
получаваме
D(Х - У) = D[Х + (-1)У] = D(Х) +
D[(-1)У] = D(Х) + (-1)2D(У) = D(Х) + D(У)
т.е.
D(Х -
У) = D(Х) + D(У)
Обърнете внимание, че няма формула за дисперсия
на произведение от случайни величи!
Използувайки свойства 1 - 7, всяка една
случайна величина може да се нормира по формулата.
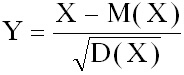 (1.3)
(1.3)
при което
М(У) = 0 и D(У) = 1
(1.4)
Задача 1. Като използвате дефиницията
за математическо очакване на дискретна случайна величина докажете
свойство 1. Упътване: фактически константата С
е дискретна случайна величина, която заема само една стойност, Х1
= C с вероятност p1
= 1. Вижте решението
на задачата.
Задача 2. Като използвате дистрибутивното
свойство на умножението (т.е. линейността на една сума) и дефиницията за
математическо очакване на дискретна случайна величина докажете свойства
2 и 3 за дискретна случайна величина. Вижте решението
на задачата.
Задача 3. Като използвате линейността
на определения интеграл и дефиницията за математическо очакване на непрекъсната
случайна величина докажете свойства 2 и 3 за непрекъсната случайна величина.
От статистиката е известно, че p(Cx)
= p(x) и p(x+y)
е p(x)
за случайната величина X
и p(y)
за случайна величина Y.
Вижте решението
на задачата.
Задача 4. Като използвате дефинициите
за математическо очакване и дисперсия на случайна величина докажете свойства
5 и 6. Вижте решението
на задачата.
Задача 5. Докажете формулите в (1.4)
с помощта на свойства 1 - 7! Вижте решението
на задачата.
Автор: Пламен
Пенчев, Ph.D.
[ това
е материал от брой 23 от септември 2008 г. на списание "Коснос" www.kosnos.com
]
 .
.



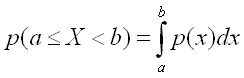
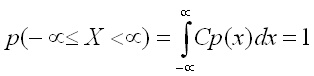
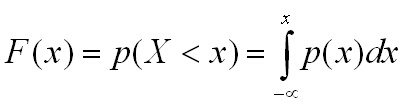

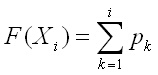



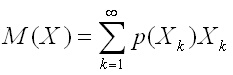 (1.1)
(1.1)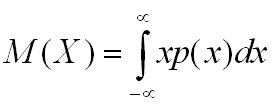 (1.2)
(1.2)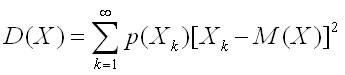
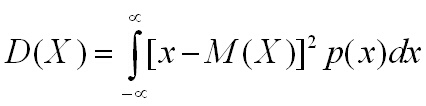
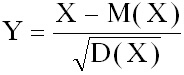 (1.3)
(1.3)