ЯМР спектроскопията е един от най-мощните методи за разгадаване на структурата на химичните съединения и за изследване на разнообразните химични процеси и реакции. Но за съжаление на български език има само две книги [2,3], които са библиографска рядкост и поради това обучението на студентите химици по дисциплината "Инструментални методи за анализ" (ИМА) е изключително затруднено. Ето защо авторът, който е ИЧ спектроскопист си позволява да състави този текст без претенциите това да е пълен авторски текст. Допълнителна смелост за написването на този материал вдъхва и четири и половина годишната работа на автора в лабораторията на проф. д-р Мортон Мънк в Държавния университет на Аризона (Morton Munk, Arizona State University), където авторът се е занимавал с компютърна интерпретация на ¹³C ЯМР спектри.

В този курс авторът следва предимно някои части от превъзходната книга на проф. Гюнтер [1], но на някои места са дадени примери, взети от други източници [4, 5], както и са вмъкнати изчисления, реализирани от самия автор.

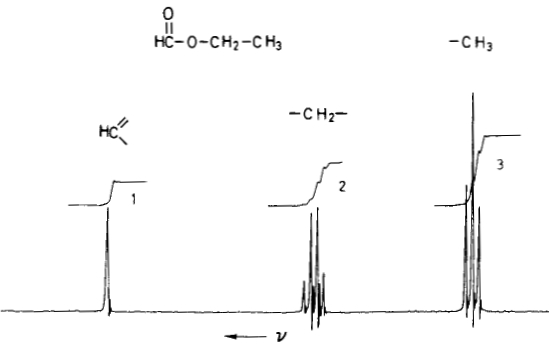
1. Що за структурна информация се съдържа в един ¹H-ЯМР спектър? На фигура 1 е даден протонният спектър на етилформиат. В следващия материал ще бъдат изяснени величините, които стоят на абцисата и ордината, но засега този спектър ще бъде разгледан предварително, за да разбере читателят колко много информация за химическия строеж на съединенията се появява в един ¹H-ЯМР спектър.

Фигура 1.¹H-ЯМР спектър на етил формиат. На абцисата е честотата при която се появяват ивиците, а на ордината - абсорбцията на радиочестотното лъчение.

Първо, в спектъра се наблюдават три групи ивици, които съответстват на химическите различни протони в съединението. От ляво на дясно това са сигналът на алдехидните протони, сигналът на метиленовите протони и този на метиловите протони. Ето затова броят на сигналите в протонния ЯМР спектър показва точно колко групи химически еквивалентни протони има в съединението, а това спомага за изясняване на структурата на съединението.

Второ, не само броят на сигналите, но и тяхното относително и абсолютно разположение по абсцисата е показателно за химичния строеж на изследваната молекула. Например, протоните, които са свързани с групи, които изтеглят електронната плътност дават ивици, които стоят в лявата част на спектъра (по-висока честота на резонанс). Това ясно се вижда от сравнението на сигналите на метиленовите протони (-CH₂-) и тези на метиловите (-CH₃): първите са по-близо до електроотрицателна група (естерната), а вторите по-далече. Освен фактора "електроотрицателност на съседните групи" върху положението на сигналите оказват влияние и други фактори, с които ще се запознаем в този и следващите материали. И точно затова положението на сигналите се използва за разкриване на структурата на изследваното съединение.

Трето, групите сигнали (наречени мултиплети) са различни по вид - сигналът на алдехидния протон е синглет (единична ивица), на метиленовите протони - квартет (четири ивици), а на метиловите е триплет (три ивици). Както ще се разбере от следващия текст, това разцепване на сигналите (при квартета и триплета) е следствие от броя на протоните, които са съседни на даващите сигнала протони. Засега ще споменем едно правило (което важи в при определени условия, но доста има изключения) и то е, че N на брой съседни протони обуславят разцепването на сигнала на N+1 ивици. Очевидно е, че това правило (както и другите, аналогични на него) спомагат за анализа на структурата на съединението.

Четвърто, относителният интензитет на сигналите в даден мултиплет следва определено правило, което се дава с т.н. триъгълник на Паскал. За двата разгледани в предния абзац мултиплети тези отношения са приблизително така както 1:2:1 за триплета и 1:3:3:1 за квартета. Тези отношения също са полезни при анализ на структурата на изследваното съединение.

Пето, площта под сигналите е пропорционална на броя протони, които дават съответния сигнал. Тази площ лесно се изчислява математически от софтуера на апарата и обикновено се дава като криви, над съответните ивици. На фигурата тези криви представляват прагове (в ляво от числата 1, 2 и 3) с отношение на височините си 1:2:3. Точно такова е и отношението на броя на съответните протони, които дават сигнала - CHO, -CH₂- и -CH₃. Несъмнено, този факт спомага за разкриване на структурата на изследваното съединение.

2. Квантово-механичен модел на протона. Ядрото на протия, ¹H, се състои от един протон. Протонът има ъглов момент P и в следствие на това, че е заредена частица има и магнитен момент m. Подобно на протона (ядрото на протия) и ядрата на много от изотопите на химичните елементи имат ъглов момент, различен от нула, и съответно имат ъглов момент. За едно ядро връзката между двете величини е:

където g се нарича магнотожироскопично отношение (старото име е жиромагнитно отношение, на английски съответно magnetogyric/gyromagnetic ratio).

Според квантово-механичната теория ориентацията на ъгловия момент на микрочастиците се квантува (има дискретни стойности) и възможните проекции на ъгловия момент P_z върху произволна ос z са равни на

където h е константата на Планк (h = 6.62610^-34Js ), а m_l е т.н. магнитно квантово число. Обикновенно h/2p се означава като буквата "хаш" зачертана във вертикалната си част, но в хипертекст документа това означение липсва и ще използваме зачертаната буква "хаш" h., т.е. P_z = hm_l.

Ако I е спиновото квантово число на ядрото, то m_l заема стойности от -I до I през единица:

Протонът има I = 1/2 и затова магнитното му квантово число може да заема две стойности: -1/2 и 1/2, а проекцията на неговия ъглов момент P_z: -h/2 и +h/2.

Съответно магнитният момент на протона ще има само две проекции m_z на произволна ос z: m_z = -gh/2 и m_z = gh/2.

На тези две проекции на магнитния момент за протона (и за някои от ядрата на химичните изотопи в самите изотопи) съответства една енергия, т.е. те са енергетически изродени. Но при поставяне в постоянно магнитно поле с магнитна индукция B₀ тяхното израждане се снема (нарушава) и тяхната енергия става съответно равна на Е = m_zB₀ = ghm_lB₀.

За протона имаме само две енергетични състояния:

Разликата между тях е DЕ = ghB₀. Обърнете внимание, че тя е право-пропорционална на магнитната индукция B₀ и нараства с нейното увеличаване, както е показано на фигура 2.

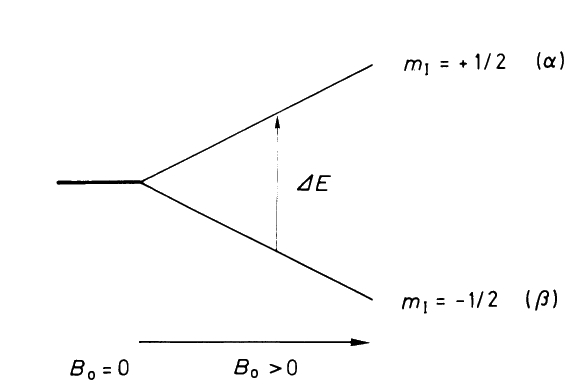
Фигура 2. Енергетичната разлика между нивата в ядрото на протия (протона), поставено в постоянно магнитно поле.

Тази енергетична разлика позволява да се осъществи преход между тези две нива при поглъщане на фотон с енергия Е = hn, равна на енергетичната разлика:

Или като съкратим константа на Планк получаваме за честотата на погълнатия фотон следния израз

Задача 1. Ако протонът има магнитожироскопично отношение g = 2.675x10⁸ Rad T^-1s^-1, да се изчисли честотата на фотона n в Hz и MHz, който ще предизвика резонансен преход при сила на полето B₀ = 1.4T. Означенията са: Rad е мярка за ъгъл, радиан; T - мярка за магнитна индукция, Тесла.

Отговор: n = 59.6x10⁶Hz = 59.6 MHz

3. Схема на ¹H-ЯМР експеримент на течности и течни разтвори. В тази точка ще дадем само най-повърхностно описание на апарат за заснемане на ¹H-ЯМР спектри, което описание ще спомогне за разбиране на последващия материал. На фигура 3 е дадена принципна схема на съответния апарат, който работи на принципа на сканирането - на английски терминът е continuous wave, непрекъсната вълна. Съвременните апарати използват импулс от радиовълни с различна честота и математическа обработка на сигналите с Фурие трансформация, но няма да бъдат разглеждани в този материал.

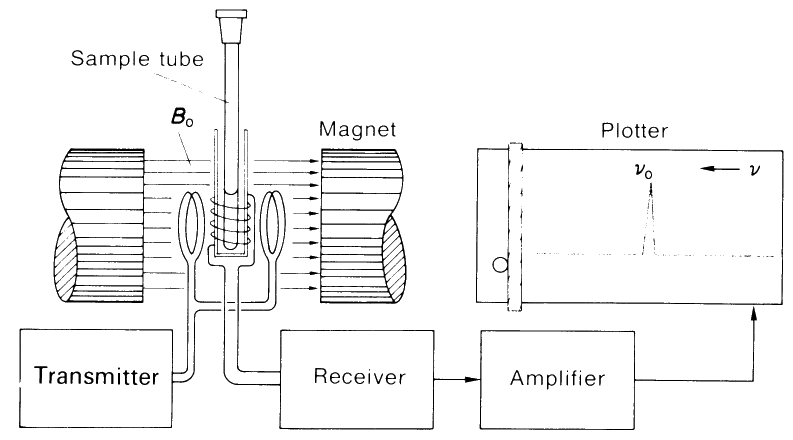
Фигура 3. Схема на ЯМР апарат с отделна бобина на предавателя и приемника. Превод на английските означения: transmitter - предавател; receiver - приемник; amplifier - усилвател; magnet - магнит; plotter - печатащо устройство; sample tube - епруветка с проба.

Пробата се поставя в тънка епруветка с дължина от около 15 cm и диаметър от 5 или 10 mm, която се завърта около своята ос за да се получи по-голяма хомогенност на магнитното поле върху пробата. От предавателя се излъчва радиочестотен сигнал, част от който се поглъща от пробата и това поглъщане се регистрира с помощта на отделна бобина - тази на приемника или от същата бобина (при апарати с една бобина). Сигналът се усилва в усилвател и се предава на печатащото устройство. За да се получи резонанс по уравнение (1) трябва или честотата на излъчваното лъчение да се променя или силата на магнита.

В този материал няма да бъдат разгледани подробно процесите на релаксация, т.е. на връщане на молекулите от възбудено в основно състояние. Само ще споменем, че енергетичната разлика между ядрата е много малка и според разпределението на Болцман те са почти еднакво заселени: по-високо енергетичното ниво е с 0.001% (т.е. с 10^-5!) по-малко населено - вижте задача 2.

Задача 2. Енергетичната разлика между ядрените нива на протия a (магнитният момент е по посока на B₀) и b (магнитният момент е в обратна посока на B₀) е DЕ = ghB₀/(2p). По формулата на разпределението на Болцман, N_a/N_b = exp(-DЕ/kT), изчислете отношението N_a/N_b  за B₀ = 1.4T. Стойностите на магнитожироскопично отношение g = 2.675x10⁸ Rad T^-1s^-1, на Болцмановата константа k = 1.38x10^-23 JK^-1 и на константата на Планк h = 6.626x10^-34 Js. Приемете че T = 298 K  (т.е. температура 25 ^oC).
! Използвайте приближението exp(-x) = 1 - x, което е вярно за малки стойности на x. Тогава разпределението на Болцман ще има вида

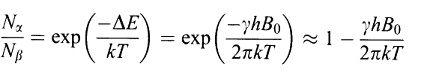
Отговор: N_a/N_b = 1 - 9.6x10^-6 = 1 - 1x10^-5, което означава че разликата в населеностите на двете нива е 0.001%, т.е. ако в долното ниво има например 100,000 молекули, то в горното ниво има 99,999 молекули.

4. Магнитни свойства на някои изотопи. Както споменахме повечето ядра на химичните изотопи на химичните елементи имат магнитен момент, различен от нула. Само ядрата, който имат четно масово число и четен пореден номер (като ¹²C, ²⁴Mg, ³²S) нямат магнитен момент - т.е. имат спиново квантово число I = 0. Това са ядрата с четен брой неутрони и четен брой протони. Ядрата с нечетен пореден номер и четно масово число имат целочислена стойност на спиновото квантово число - например ¹⁰B, ¹⁴N и ²H. В таблица 1 са дадени някои свойства на част от нуклеидите.

Таблица 1. Свойства на част от нуклеидите. Превод на английските означения: nucleus - ядро; spin quantum number - спиново квантово число; magnetic moment - магнитен момент (той е даден в единицата ядрен магнетон, m_N = 5.050^-27 J T^-1); resonance frequency - резонансна честота, тук тя е изчислена при сила на магнитното поле 1 T; relative sensitivity - относителна чувствителност, тук спрямо протонния резонанс; natural abundance - природно разпространение, тук в молни проценти; quadrupole moment - квадруполен момент.

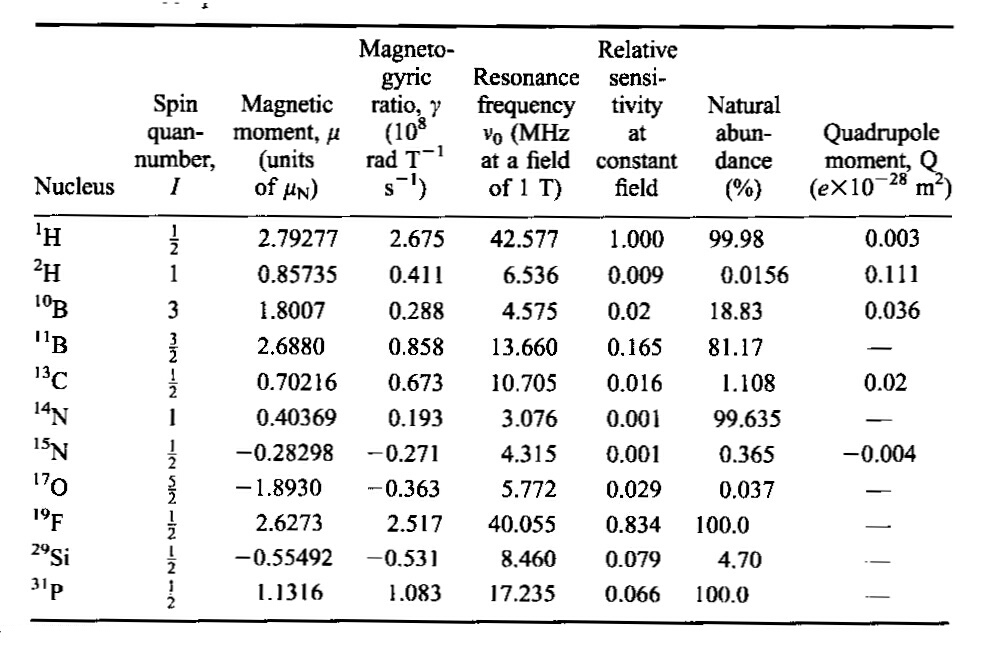
По принцип е възможен ЯМР експеримент със всички ядра, които имат спиново квантово число, различно от нула. Най-разпространени са техниките, които включват ЯМР с ядрата на протия и ¹³C, както и ¹⁵N, ¹⁷O и ³¹P. Трябва да се подчертае, че в един експеримент не е практически възможно да се регистрират едновременно резонансите на няколко типа ядра (например тези на ¹H и ¹³C) и затова това не се прави, а се заснемат различните спектри при различни експерименти, макар и на един и същ апарат. Този факт като и различната резонансна честота на деутерия от протия дава възможност да се използват деутирирани съединения като разтворители в H-ЯМР спектроскопията: най-използваните са тежка вода (D₂O), бензен-D₆, CDCl₃ и CD₃SOCD₃.

1. Harald Gunter. NMR-Spektroscopie: Grundlagen, Konzepte und Anwendung der Protonen und Kohlenstoff-13 Kernresonanz-Spektroscopie in der Chemie. Georg Thieme Verlag, Stuttgart, 1992.

2. Ст. Спасов, М. Арнаудов. Приложение на спектроскопията в органичната химия, Изд. "Наука и изкуство", София, 1978.

3. Ст. Спасов, Л. Каменов. Ядрен магнитен резонанс в органичната химия, Изд. "Наука и изкуство", София, 1973.

4. Eberhard Breitmaier. Structure Elucidation By NMR In Organic Chemistry: A Practical Guide. John Wiley & Sons, Ltd., 2002.

5. Joseph B. Lambert, Eugene P. Mazola. NMR_Spectroscopy. Pearson Eduaction Inc., 2001.

Кредити: фигури 1, 2 и 3 и таблица 1 са взети от книгата на Гюнтер [1].

Автор: Пламен Пенчев, Ph.D.