За най-малките (пък и не само за тях) – Компютрите през погледа на проф. Процесор Аритметиков

Двоичните числа (продължение)

Миналия път се запознахме с двоичните числа, които са съставени само от две цифри – нула и едно. Научихме, че първите няколко числа са 1, 10, 11, 100, 101 и т.н. Лесно ги съставихме – просто в двоичната система няма цифрите 2, 3, и останалите цифри до девет. Отбелязахме, че ще видим как двоични числе се превръщат в десетични и обратно. Сега точно с това ще се занимаем, но нека започнем с познатите ни десетични числа.

Когато запишем, например, числото 265 имаме предвид, че сме сумирали две стотици, шест десетици и пет единици, т.е. 265 е съставено по следния начин (с x означаваме операцията умножение):

265 = 2 x 100 + 6 x 10 + 5 x 1

Всъщност 100 е равно на 10², 10 е равно на 10¹, а 1 ... на 10⁰. (Да – всяко положително число, повдигнато на нулева степен дава единица!) Затова горното представяне на числото 265 може да се запише така:

265 = 2 x 10² + 6 x 10¹ + 5 x 10⁰

И в това няма нищо чудно! Нали говорихме за десетичната система?! Всяко едно число е сума от съответните степени на 10 умножени по цифрите в него. И тези степени започват от нула (и са нула за единиците) и нарастват с едно наляво – 0, 1, 2 и т.н.

Както се досещате числото 1,048,576 се записва по следния начин (със запетайка са разделени всеки три цифри за по-добра четимост на числото – иначе десетичната точка ще я означаваме така, както американците я означават – с точка “.”, а не със запетайка “,”):

1,048,576 = 1 x 10⁶ + 0 x 10⁵ + 4 x 10⁴ + 8 x 10³ + 5 x 10² + 7 x 10¹ + 6 x 10⁰

По същата логика двоичната система има за основа числото 2, както десетичната има за основа 10. Следователно двоичните числа означават аналогични суми, но на степените на числото 2.

1 = 1 x 2⁰ = 1 x 1 = 1

10 = 1 x 2¹ + 0 x 2⁰ = 1 x 2 + 0 x 1 = 2 + 0 = 2

11 = 1 x 2¹ + 1 x 2⁰ = 1 x 2 + 1 x 1 = 2 + 1 = 3

и т.н.

101 = 1 x 2² + 1 x 2¹ + 1 x 2⁰ = 1 x 4 + 0 x 2 + 1 x 1 = 4 + 0 + 1 = 5

Може би си спомняте една таблица от миналата лекция за съответствието между двоични и десетични числа – сега ще я запишем по-подробно:

Десетично число	Двоично число	сума
1	1	1 x 2^0
2	10	1x2^1 + 0x2^0
3	11	1x2^1 + 1x2^0
4	100	1x2^2 + 0x2^1+ 0x2^0
5	101	1x2^2 + 0x2^1+ 1x2^0
6	110	1x2^2 + 1x2^1+ 0x2^0
7	111	1x2^2 + 1x2^1+ 1x2^0
8	1000	1x2^3 + 0x2^2 + 0x2^1+ 0x2^0
9	1001	1x2^3 + 0x2^2 + 0x2^1+ 1x2^0
10	1010	1x2^3 + 0x2^2 + 1x2^1+ 0x2^0

Малко по-сложно е от десетична система да се премине в двоична система. Очевидно, първо трябва да намерим най-високата степен, с която като повдигнем на число 2 получаваме число, което не надминава десетичното число. За десетичното 10 тази степен е 3, т.е 2³ = 8, което е по-малко от 10, докато 2⁴ = 16, което е по-голямо от 10 (десетичното десет). Следващата стъпка е да извадим това число от десетичното число – за този пример получаваме 10 – 8 = 2. Е, получихме 2, което е 2¹, т.е. 10 = 2³ + 2¹ = 8 + 2. А по логиката, дадена по-горе това е числото

10 = 1 x 2³ + 0 x 2² + 1 x 2¹ + 0 x 2⁰ = 8 + 0 + 2 + 0

т.е. това е двоичното число 1010 (сравнете този запис с тези от таблица по-горе!)

Нека потренираме този алгоритъм с едно по-голямо число – 233. Почваме със степените на двойката

2⁰ = 1, 2¹ = 2, 2² = 4, и т.н. 2⁷ = 128, 2⁸ = 256. Последното число, 256, е по-голямо от 233, значи ще работим с 2⁷ = 128. Изваждаме 128 от числото, което ще превръщаме и получаваме

233 – 128 = 105

Същото повтаряме за полученото число: 2⁶ = 64 < 105 и като ги извадим ще получим

105 – 64 = 41

За 41 получаваме аналогично 2⁵ = 32 < 41

41 – 32 = 9

За 9 пък имаме 2³ = 8 < 9, т.е изваждаме 9 – 8 = 1, което e 1 = 2⁰.

Забелязахте ли, че постоянно изваждахме степени на двойката от числото докато получим единица или нула (както бе в примера за десетичното 10)? Кои степени на двойката изваждахме докато получим 1? Извадихме 2⁷, 2⁶, 2⁵, 2³, и 2⁰. А това означава, че нашето десетично число се състои от тези умалители (които изваждахме от него за да получим нула), т.е.

233 = 2⁷ + 2⁶ + 2⁵ + 2³ + 2⁰ = 1x2⁷ + 1x2⁶ + 1x2⁵ + 0x2⁴ + 1x2³ + 0x2² + 0x2¹ + 1x2⁰

или

233 = 11101001

или за да стане това разлагане по-ясно, то е показано по-долу на картинката

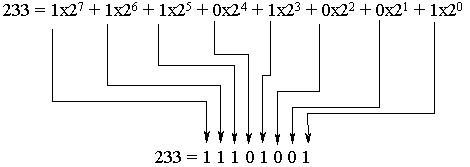
На практика това превръщане може да се направи с калкулатора на Windows. Стартираме калкулатора и написваме десетичното число като внимаваме радиобутона Dec да е включен.

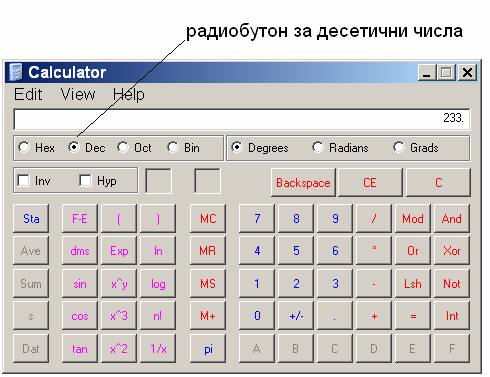
След което натискаме радиобутона Bin и получаваме 11101001.

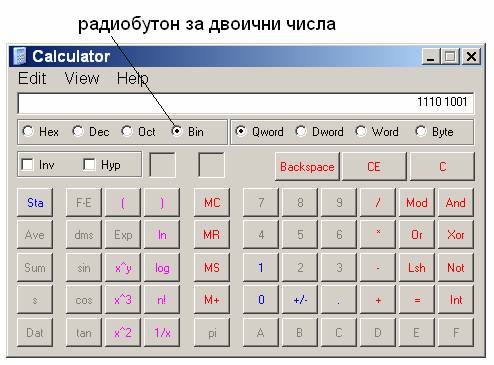
Разбира се, че можем да се върнем обратно в десетично число. А това означава, че можем да напишем двоично число и да го превърнем в десетично.

Следващия път ще научим шестнадесетичната бройна система, в която числото 10 се представя като буквата A, а 11 като B и т.н. C, D, E, и F за числото 15. Тя също се използва в компютрите и то особенно при работа с адресите на паметта или адресите на файловете на различните дискови устройства.

Малко английски

И последно – в компютърните програми в повечето страни по Света се пише на английски. Затова нека видим как са на английски някои от думичките, с които се запознахте днес.

български	английски	произнасяне	български	английски
степен	power	пауър	на n-та степен	to the n-th degree
степен	degree	дигрии	повдигам на трета степен	raise to the third power

[ това е статия от брой 2 на списание "Коснос" www.kosnos.com]