Нека имаме комплексно съединение с формула ML₄, което има равнинна квадратна структура с лигандите L разположени по върховете на квадрат. Да допуснем че това съединение има диполен момент, означен с вектора m и този диполен момент не лежи на оста на симетрия, която току що разгледахме в другия материал. Тогава при завъртане на 90 градуса този диполен момент се завърта и реално показва, че е извършена ротация с молекулата, противно на твърдението, че не може да се познае дали има такава след една операция на симетрия.

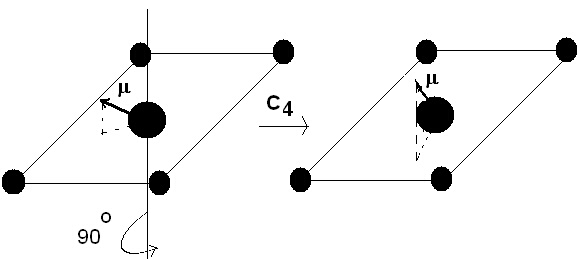
За да няма промяна, единствената възможност е този диполен момент да е разположен по остта на симетрия. Както ще видим в предишния материал, тази химична структура има още няколко операции на симетрия, една от които е завъртане на 180^o по ос, перпендикулярна на вече използвана ос. Това завъртане ще преобразува вектора на диполния момент, m, в противоположен на него: -m.

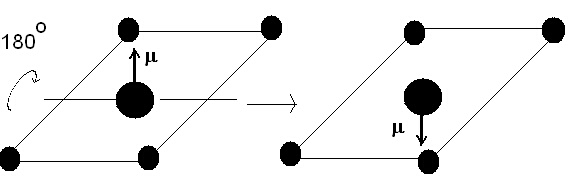
Тази промяна на диполния момент след операция на симетрия показва, че той трябва да е равен на нула. Следователно молекулите с това разположение на лигандите нямат диполен момент. Видяхме как с представата за симетрия получихме едно теоретично предсказание, което се потвърждава от експеримента.

Обратно в основния текст