Симетрия на молекулите

част първа

Операции на симетрия

Симетрията е представа (концепция), че някакъв обект не се променя при извършване на така наречените "операции на симетрия". Например един квадрат може да бъде завъртян на 90 градуса по ос, перпендикулярна на равнината и минаваща през центъра му и той няма да бъде променен.

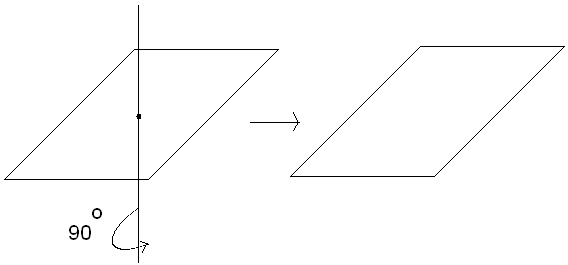
Или казано с други думи, човек не може да разбере с наблюдение на квадрата само в първоначалната и последващата позиция, че той е бил завъртян. Или формулирано по-точно, човек не би могъл да разбере с никакви научни методи (а наблюдението е един от тях), че върху дадения обект е извършена операция на симетрия. Именно в тази особеност се крие ценността на операциите на симетрия за науката, както ще видим по-късно. (Ако сте любопитни колко е мощна концепцията за симетрия натиснете ТУК за да видите само с тази дефиниция колко обхватен извод можем да направим за диполния момент на квадратни комплексни молекули от вида ML₄)

Но нека се запознаем първо с операциите на симетрия. С една от тях вече се срещнахме - завъртане под даден ъгъл. Целият равнинен ъгъл е 360^o и завъртането на 90^o представлява завъртане на 1/4 от този ъгъл, затова тази операция на симетрия се означава със символа C₄. Остта на завъртане се нарича елемент на симетрия и в случая представлява ос на симетрия от четвърти порядък. Какви други оси на симетрия има квадратът? Ето още две оси на симетрия, но те са от втори порядък, C₂.

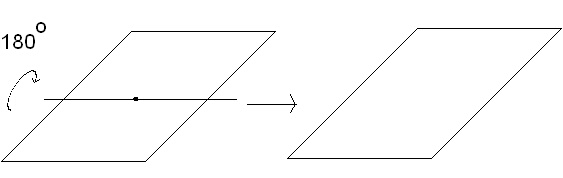
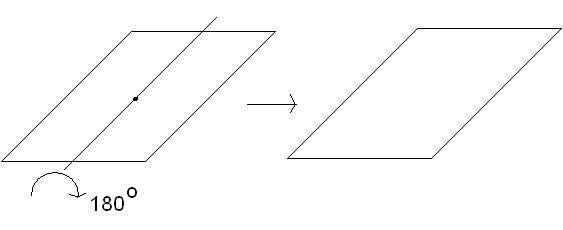
И така, ос на симетрия от n-ти порядък, C_n, се нарича ос, по която тялото завъртяно на ъгъл 360/n градуса се отзовава в идентична конфигурация (положение). И понеже говорим за симетрия на молекулите, съответните операции ще бъдат извършвани върху молекули. С букви ще означаваме идентичните атоми в молекулата за да проследим резултата от съответната операция на симетрия. Например за водната молекула операцията на симетрия C₂ дава следната размяна между двата водородни атома

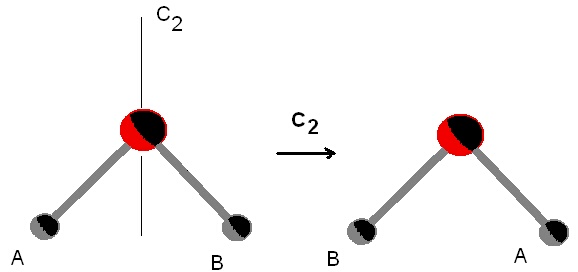
(операциите на симетрия ще ги изписваме надебелен шрифт ето така C₂, за да ги различаваме от съответните им елементи - C₂)

Кои са другите елементи на симетрия и техните съответни операции на симетрия? Следващият елемент е равнина на симетрия, която се означава с гръцката буква "сигма" s, а съответната операция се нарича отражение в равнина на симетрия, s. Всъщност, тази операция е подобна на отражението ни в огледало, но с тази разлика, че огледалото не минава през нас.

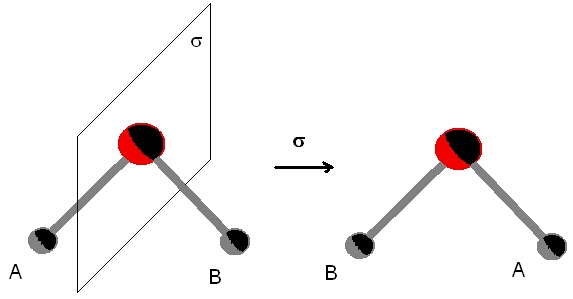
Както се вижда от рисунката, в тази равнина лежи кислородният атом и тя е перпендикулярна на правата, която свързва двата водородни атома.

Молекулата на водата има още една равнина на симетрия - досетихте ли се? Да, това е равнината, в която са разположени атомите на молекула. Тя изобразява всеки един атом в себе си. Тези два елемента на симетрия се наричат вертикални равнини на симетрия, тъй като остта C₂ лежи във всяка една от тях -- т.е. тя е пресечната права на тези две перпендикулярни една на друга равнини.

Както казахме, втората равнина на симетрия изобразява всеки един атом в себе си, и това е следствие от разположението на атомите в тази равнина. Но има една подобна операция на симетрия, която се нарича операция на идентичност, която запазва положението на атомите в молекулата непроменено. Тя се бележи с Е. За какво е необходима такава операция, която не извършва нищо? Обяснението е математическо и е аналогично на това, защо има числото 0, което добавено към кое да е число дава същото число, или защо има числото 1, което умножено по кое да е число дава същото число. Всъщност, тези четири операции на симетрия за молекулата на водата образуват една група на симетрия - група е името на специална структура в математиката, в която обектите (в случая операциите на симетрия) се подчиняват на дадени правила.

Групата на симетрия на водата се означава C_2v, и в нея има четери операции - Е, C₂, s_v и s^'_v. Втората равнина на симетрия се бележи с прим, а долният индекс "v" идва от английската дума vertical.

Има още две операции на симетрия, които ще демонстрираме с молекулите на етена (H₂C=CH₂) и на алена (H₂C=C=CH₂). Първата молекула е равнинна - т.е. всички атоми лежат в една равнина, а при втората молекула трите въглеродни атома лежат на една права, но четирите водородни атома не лежат в една равнина. Те два по два са разположени в две взаимно перпендикулярни равнини, които се пресичат в правата, по която са разположени трите въглеродни атоми.

Операцията отражение спрямо (през) център на симетрия,i, изпраща даден атом по правата, която минава през него и центъра на симетрия, на разстояние от атома до центъра i, равно на предишното разстояние между тях.

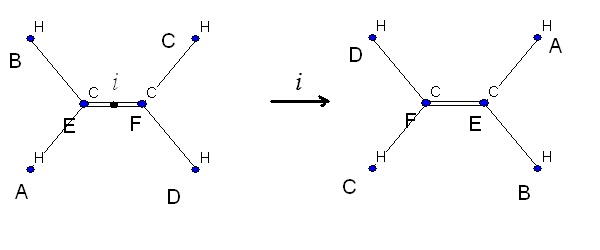
В резултат на тази операция при етеновата молекула, двата въглеродни атома сменят своите места (F преминава в E и Е в F), а водородният атом с означение A заема мястото на водородния атом C и т.н.

Последната, пета операция на симетрия, се нарича несобствено завъртане (или огледална ротация). Отбелязва се с S_n и означава завъртане на молекулата по дадена ос на 360/n градуса и последващото отражение в равнина, която е перпендикулярна на тази ос. Ето как операцията S₄ променя разположението на атомите в молекулата на алена.

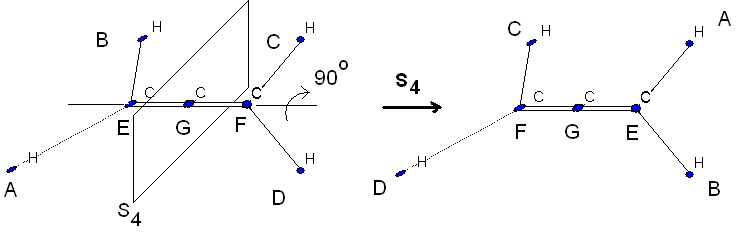
Няма значение коя част от операцията се извършва първо - завъртането и после отражението дават същия резултат както първо отражение, а после завъртане. Както се вижда от горната рисунка, в лявата молекула (преди операцията) атомите A и B лежат в равнина, перпендикулярна на равнината на рисунката, а атомите C и D - в равнината на рисунката. При завъртане на 360/4 = 90 градуса водородният атом с означение C минава зад рисунката и при последващото отражение преминава на мястото на атома B. Така всички водородни атоми имат нови позиции, а въглеродните атоми E и F разменят своите места, докато въглеродният атом G остава на своето място. Това е така, защото той лежи и на оста на завъртане и в равнината на отражение. Оста на завъртане, както се вижда, минава през трите въглеродни атома, а равнината на отражение е перпендикулярна на тази ос и минава през атома G.

Интересно е да се отбележи, че отражението през център на симетрия,i, дава същите резултати като операцията S₂: това лесно може да се провери на рисунката на етановата молекула, където е показано отражение през център на симетрия. Но въпреки това, операцията i има свое собствено означение и се описва с едно действие, а не с поредица от две.

Е, запознахме се със всички операции на симетрия. Всички те оставят една точка (и тя е една и съща) с непроменено положение. Т.е. даже в една молекула да има от всички видове операции, то точката, която съвпада с центъра на симетрия остава непроменена при всички тях. Затова тези групи на симетрия се наричат точкови групи на симетрия.

И накрая нека видим първите приложения на операциите на симетрия към експериментално определяния диполен момент на молекулата. Ако сте били любопитни и сте прегледали този материал, то вече знаете че комплексно съединение с формула ML₄, което има равнинна структура с лигандите L разположени по върховете на квадрат, има нулев диполен момент. Нека сега представим малко повече подобни изводи! Първо, ако молекулата има ос на симетрия, то диполният момент трябва да лежи на тази ос. Второ, ако молекулата има две различни оси на симетрия (представени от несъвпадащи се прави), то диполният момент трябва да лежи на всяка една такава ос и понеже това е невъзмoжно, то той е равен на нула. Трето, ако молекулата има център на симетрия то тя трябва да няма диполен момент - в противен случай , m би се преобразувал при операцията отражение през центъра на симетрия в противоположния си вектор: -m.

Автор: Пламен Пенчев, Ph.D.
Авторски права: Материалът или част от него могат да се използват свободно (копирани на друг сайт) в обучението на български или македонски студенти само ако в сайта изрично се цитира тази оригинална статия във вида: П.Пенчев, Симетрия на молекулите. Част 1., Списание "Коснос", брой 2, 2006 г. http://www.kosnos.com