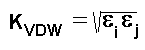
EMMX = S ESTR(i, j) + S EBND(i, j, k) + S ETOR(i, j, k, l) + S ES-B(i, j, k) + S EVDW(i, j) + S EDIP(a, b) (1.1)
Сумирането в първата сума се извършва по всички двойки (i, j) свързани атоми в молекулата, i < j; във втората сума - по всички тройки (i, j, k) атоми, които са свързани с поне две връзки в реда i - j - k; в третата - по всички четворки атоми, които са свързани с поне три връзки в реда i - j - k - l. Сумирането в четвъртата сума се извършва аналогично на това във втората - по всички тройки (i, j, k) атоми, които са свързани с поне две връзки в реда i - j - k. В петата сума сумирането е по всички двойки атоми (i, j), i < j, които се намират в 1-4 положение, 1-5 положение и т.н. Това означава, че Ван-дер-Валсовите взаимодействия не се отчитат за свързани атоми (1-2 и 1-3 разположените атоми). Последната сума е по всички двойки диполи в молекулата (a, b), a < b.
Константата KS се нарича еластичност (силова константа) на химичната връзка, и ако ESTR се измерва в Kcal / mole, а r и r0 са в Ang (ангстрьом, 1 Ang = 10-10 m), то размерността и е очевидно в Kcal / (mole Ang2). Ако молекулата е съставена от два атома и не се отчитат другите видове взаимодействия, параметърът r0 може да се приеме за равновесната дължина на химичната връзка: в този случай EMMX = ESTR, а енергията има минимум за r = r0, който очевидно по уравнение (1.2) е равен на нула. При наличие на другите енергетични членове, дължината на връзката за която EMMX има минимум е различна от r0, и ето защо последният параметър само условно може да се нарече равновесна дължина на химичната връзка.
При големи отклонения на r от r0 обикновенно се използва само квадратичния член във формула (1.2)
ESTR(i, j) = 71.94 KS (r - r0)2,
с цел да не се получават отрицателни стойности. Членът от трета степен по (r - r0)
ESTR(i, j) = 71.94 KS (r - r0)2 [ - 2.0 (r - r0)] = - 143.88 KS (r - r0)3
се добавя в краен етап на изчисленията, когато |r - r0| < 0.5, при което винаги имаме ESTR> 0.0.
Параметрите KS и r0 са табулирани в отделен файл, използван от програмата PCModel. Те са определени за всяка двойка валентни състояния на атомите. Стойностите на тези параметри в полето MMX (1986 г.) могат да се видят тук.
! свободните електронни двойки към кислородните, азотните и др. атоми се разглеждат в полето MMX на програмата PCModel като отделен "атом" (# 20), при което разстоянието между тях и съответния атом също се варира.
EBND(i, j, k) = 0.021914 KB (q - q0)2 [1 - 7.0 10-8 (q - q0)4] (1.3)
Константата KB се нарича силова константа на валентния ъгъл, и ако EBND се измерва в Kcal / mole, а q в grad (градуси), то размерността и е очевидно в Kcal / (mole.grad2). Параметърът q0 може да се приеме за равновесната стойност на валентния ъгъл, ако молекулата е съставена от три атома (X-Y-Z) и се отчитат само стретчинг и бендиг взаимодействията (ESTR и EBND); в този случай EMMX = ESTR + EBND, и енергията има минимум при едновременно изпълнение на r = r0 и q = q0. За молекули с повече от три атома се отчитат и останалите енергетични членове (торзионните потенциали, дипол-диполни, стретчин-бендиг и Ван дер Валсовите взаимодействия), и тогава стойността на валентния ъгъл за която EMMX има минимум е различна от q0: ето защо последния параметър само условно може да се нарече равновесна стойност на валентния ъгъл.
Параметрите KB и q0 са табулирани в отделен файл, използван от програмата PCModel. Те са определени за всяка тройка валентни състояния на атомите. Стойностите на тези параметри в полето MMX (1986 г.) могат да се видят тук.
! свободните електронни двойки към кислородните, азотните и др. атоми се разглеждат в полето MMX на програмата PCModel като отделен "атом" (# 20), при което валентният ъгъл "с тяхно участие" също се варира.
ETOR(i, j, k, l) = 1/2 [V1(1 + cosw) + V2(1 - cos2w) + V3(1 + cos3w)] (1.4)
С w (в rad) е означен диедричният ъгъл, образуван от четирите атома.
Параметрите Vk са табулирани в отделен файл, използван от програмата PCModel. Те са определени за всяка четворка валентни състояния на атомите. Стойностите на тези параметри в полето MMX (1986 г.) могат да се видят тук.
! свободните електронни двойки към кислородните, азотните и др. атоми се разглеждат в полето MMX като отделен "атом" (# 20), при което диедричният ъгъл "с тяхно участие" също се варира.
rA, rA0 и rB, rB0 са дължините на връзките между атоми i, j и j, k и техните "равновесни" стойности, q и q0 е валентният ъгъл между връзките и неговата "равновесна" стойност. KS-Bе параметър, който се определя не за всяка отделна тройка атоми, а по следния начин:
Обиковенно потенциалната функция на взаимодействие се апроксимира с т.н. 6-12 или 6-exp потенциали:
EVDW = a r-6 - b r-12 или EVDW = c r-6 - d exp(- f r)
където a, b, и съответно c, d и f са параметри, които се нагласяват емпирично, така че разстоянието между атомите, за които потенциалът има минимум и дълбочината на този минимум да съответстват на експерименталните данни. Първите части и в двете формули съответстват на силите на отблъскване, докато вторите - на силите на привличане.
В полето MMX Ван-дер-Валсовото взаимодействие между два атома i, j се представя със следната потенциална функция:
EVDW(i, j) = KVDW[2.25.P6 - 2.90.105.exp(-12.50/P)] (1.6)
където P е отношението на сумата от Ван-дер-Валсовите радиуси на взаимодействащите си атоми и разстоянието между тях: P = (ri + rj) / ri,j. Ако се замести P в израза (1.6) ще се получи формула от вида EVDW = a r-6 - b exp(-c r) - следователно в ММХ полето се използва 6-exp потенциал.
От израза за изчисляване на P се вижда, че се използват параметри на отделните атоми - техните Ван-дер-Валсовите радиуси, ri. С цел намаляване на параметрите, също и константата KVDW се представя като комбинация (средно геометрично) от отделни атомни параметри, ei, наречени еластичности на атомите:
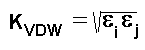
Параметрите ei и ri са табулирани в отделен файл, използван от програмата PCModel. Те са определени за всяко едно валентно състояние на атомите. Стойностите на тези параметри в полето MMX (1986 г.) могат да се видят тук.
! водородният атом в свързано състояние има само една електронна двойка около себе си, и тя е предимно изтеглена по дължината на връзката. Това изтегляне значително измества областта, която е заета от сферата, определена от неговия Ван-дер-Валсов радиус. Ето защо, преди изчисленията по формула (1.6), положението на водородните атоми в молекулата се преизчислява, като тези атоми се преместват по направлението на връзката, към атомите, към които те са свързани. Съответно, X-H връзките се скъсяват с коефициент 0.915.
За два дипола с номера a, b енергията на взаимодействие между тях се дава със следния израз:
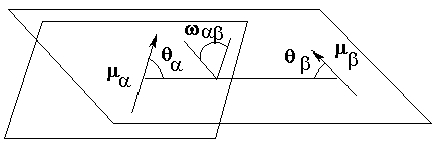
EDIP(a, b) = (mamb) [cos(wa,b) - cos(qa) cos(qb)] / (D ra,b3) (1.6)
където ma и mb са съответните частични диполни моменти по връзките, а ra,b е разстоянието между центровете на диполите. D е така наречената диелектрична константа и нейната стойност няма никаква връзка с константата за кое да е вещество: нейната стойност е нагласена емпирично на D = 1.50, с цел добро съгласуване на оптимизираните геометрични параметри на молекулата с експерименталните. Ъглите в cos() функциите са показани на следната рисунка:
! величините ma и mb нямат нищо общо със някакви експериментално измеряеми подобни стойности. По принцип е възможно измерването на диполния момент на неутрална молекула, но не и отделни негови съставящи по химичните връзки. Стойностите, които са параметризирани за полето MMX, дават добро възпроизвеждане на дипол-диполното взаимодействие, и освен това, събрани векторно след оптимизиране на геометрията дават много добро възпроизвеждане на диполния момент на молекулата.
[ това е статия от брой 5 на списание "Коснос" www.kosnos.com]