Хемометрика
Пространство на образите и мерки за разстояние в него

Теоретични задачи

Задача 1. Спектърът от фигура 1 е разделен на 7 интервала с различна дължина. Определете на око приблизителната стойност на седемте признака, които представляват абсорбцията на максималния пик в интервала.

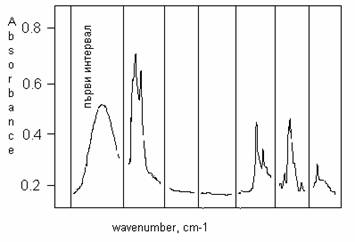
Фигура 1. ИЧ спектър на 1-нонанол.

Задача 2. Колко петмерни образа биха се получили от 18-те данни от фигура 2, ако се взимат четирите измервания предхождащи часа и измерването в часа. Кои са другите възможни начина при взимане на пет поредни измервания на концентрацията? Съответно колко образа се получават при всеки начин на съставяне на образите?

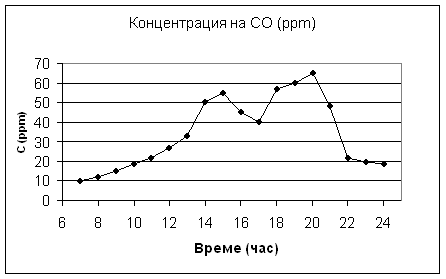
Фигура 2. Концентрацията на въглеродния моноксид като функция от времето.

Задача 3. Кодирайте двоично цифрата 0, дадена на изображението по-долу. Колко е размерността на изображението? Колко е размерността на образа? Колко е стойността на x₁₂, x₂₃ и x₄₉?

Задача 4. Какъв е химическият смисъл на диагоналната линия (минаваща през точката с координати (0, 0) и точката (70, 70) на фигура 3 ? Каква е разликата между точките над нея и под нея? Какъв най-общ признак обединява точките в близост до началото на координатната система? Каква е разликата между тях и точките в близост до точката (70, 70) ?

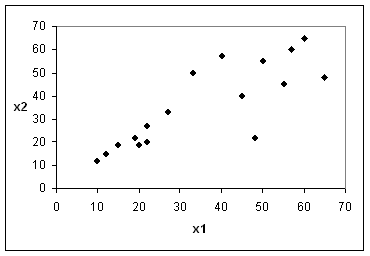
Фигура 3. Двумерното пространство на двумерни хемометрични образи, съставени от събитията от фигура 2. На първата координата е концентрацията на CO един час преди текущото измерване, а втората – концентрацията в часана измерването.

Задача 5. Имате три двоични петмерни образа, X₁ = (1, 1, 0, 1, 0), X₂ = (0, 0, 1, 1, 0) и X₃ = (0, 1, 1, 1, 0). Изчислете следните разстояния между тях: D₁, D₂, D_H и D_T. [за означенията вижте формули (2) – (4) в лекцията ]

Задача 6. Кое от разстоянията на Минковски (M = ?) отговаря на разстоянието по Хеминг? Какво показва разстоянието по Хаминг?

Задача 7*. Разглежданите мерки за разстояния са частен случай на мерки за разстояния, които математиците въвеждат в едно N-мерно векторно пространство. Ако X_K, X_L и X_M са три кои да е вектора в пространството, то всяка реална функция от тях D(X_K,X_L), която изпълнява следните отношение, може да се приеме за мярка за разстояние:

1. D(X_K, X_L) ≥ 0; (мярката е неотрицателна)
2. D(X_K, X_L) = D(X_L, X_M); (мярката не зависи от посоката на изминавана на разстоянието)
3. D(X_K, X_L) = 0 само ако X_K = X_L; (тя е нула само за съвпадащи вектори)
4. D(X_K, X_L) + D(X_L, X_M) ≥ D(X_K, X_M). (неравенство на триъгълника – сумата от две от страните му е винаги по-голяма от третата или равна ако трите точки лежат на една права)

Проверете отговарят ли всички разстояния на тези условия. Проверката на условие 4 аналитично е трудна задача, затова проверете дали изчисленията от задача 5 не му противоречат.

Автор: Пламен Пенчев, Ph.D.

[ това е материал от брой 13 на списание "Коснос" www.kosnos.com]