Още с навлизането на първите компютри в химичните лаборатории в началото на седемдесетте години се зароди нова химична дисциплина, наречена хемометрика (chemometrics). Най-общо хемометриката може да бъде дефинирана [1] като химична дисциплина, която използва математически и статистически методи, както и методите на формалната логика и теорията на информацията за максимално извличане на пълноценна химична информация при анализа на химични данни. С този материал започваме една поредица, която ще ни разкрие основните хемометрични методи и тяхното приложение в химията и спектроскопията.
Има много курсове по хемометрика и нейните методи [1-5], включително и на български [6,7], но ние ще следваме по структура превъзходния курс на професор Вармуца [2]. За съжаление в България няма съгласие относно името на тази дисциплина: понеже е химическа, някои предлагат да се казва химиметрия, и понеже българските окончания са на -ия, то предлагат и името хемометрия, но според мен подобно на предишно-възприетата чужда дума, биометрика, то е по-благозвучно тя да се наименова буквално от английския си правопис - хемометрика. Също така английските термини ще бъдат давани след техния български превод - това не само допълнително пояснява значението на думата, но и спомага на учещите да се запознават с термините на езика, който се използва по целия свят.
Ще започнем с едни от основните понятия - пространство на образите и мерки за разстояние в него, които съставят азбуката на хемометриката.
1. Химични образи. Един химичен обект или събитие се представя в пространството на образите като наредена енторка от числа, (x1, x2, … xN), която се нарича образ (pattern), а пространството (най-общо то е N-мерно) се нарича пространство на образите (pattern space). Отделните числа, xk, се наричат характеристики или признаци на образа (features). Всяко едно от тях представлява резултат от измерването на дадена величина, която характеризира химичния обект или химичното събитие. Тази наредена енторка от числа преставлява N-мерен вектор, а самите признаци са координатите на този вектор.
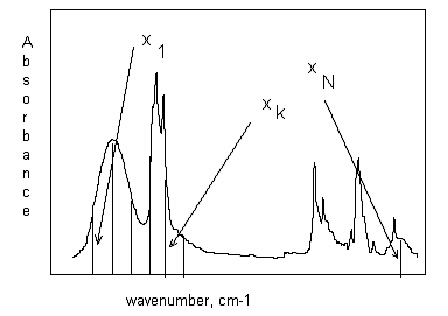
Пример за химичен обект е инфрачервения (ИЧ) спектър на едно вещество. На фигура 1 е даден ИЧ спектър на 1-нонанол. Ако целият спектрален интервал се раздели на N - 1 интервала, то стойностите на абсорбцията при техните граници (N на брой) представляват отделните признаци. Тези интервали могат да бъдат с еднаква големина (еквидистантни интервали) или с различна големина.

Фигура 1. ИЧ спектър на 1-нонанол. Височините на вертикалните линии, които отчитат величината на абсорбцията при определени вълнови числа се взимат за признаци на образа.
Пример за поредица от химични събития е стойността на концентрацията на дадено вещество във въздуха, като функция от времето. На фигура 2 е дадена концентрацията на въглеродния моноксид на определено кръстовище в Пловдив през деня като функция от времето.
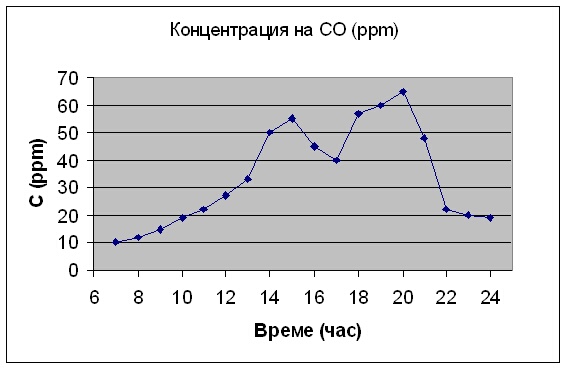
Фигура 2. Концентрацията на въглеродния моноксид като функция от времето.
В този случай отделният химичен образ може да се състави по няколко начина – например стойността на концентрацията в дадено време представлява едномерен образ, x1. Но могат да се образуват и тримерни химични образи, съставени от три съседни концентрации – например химичния образ, който отговаря на 14 часа е съставен от концентрациите на CO, измерени в 13, 14 и 15 часа. Разбира се, че цялата графика, съставена от 18 стойности, може да се приеме за едно събитие, в този случай 18-мерно събитие, което характеризира замърсяването на кръстовището през този ден с въглероден моноксид.
2. Двоични образи. Това са образи
съставени от признаци, които могат да заемат само две стойности, например
0 и 1, или -1 и 1. Пример за такъв образ е графичното числено изображение
да дадена чернобяла фигура, наречено цифрово двоично изображение
или образ (digital binary image). На фигура 3 е дадено изображението
на цифрата 2.
 |
Фигура 3. Цифрово изображение на цифрата 2 с разделителна способност 8 x 7. |
Изображението е с разделителна способност
8 на 7 точки (pixels), т.е. реално в цифрова форма то представлява
една матрица с размери 8 реда (rows) на 7 колони (columns),
чиито елементи dr,c
са 1 (черен цвят) или 0 (бял цвят). В този случай това изображение може
да се превърне по няколко начина в образ, като най-елементарният е признаците
да се получат от матричните елементи чрез взимането на последните по редове.
Общата формула в този случай е x
7x(r-1)+c
= dr,c, т.е. x1
= d1,1,
x2
= d1,2,
…, x32
= d5,4
и т.н до x56
= d8,7.
За изображението на фигура 3 се получава следния двоичен образ, представен
на фигура 4.
| 0011111
0010001 0010001 0000001 0011111 0010000 0010000 0011111 |
... | Фигура 4. Двоичният образ на цифрата 2; векторът е представен в осем реда по 7 цифри като са изпуснати запетаите между отделните признаци, xk. |
При някои от използваните методи нулата като стойност на признак е неудобно число, защото умножението с нея дава нула, и тогава тя се заменя с -1: в този случай двоичният образ е съставен от признаци, които приемат стойности само -1 и 1.
3. Пространство на образите. Ако на всеки признак, xk, на хемометричния образ (x1, x2, … xN) се съпостави една от координатите в N-мерното пространство, то хемометричният образ преставлява един N-мерен вектор, а самите признаци са координатите на този вектор. Това пространство се нарича пространство на образите (pattern space). Например от концентрациите на въглеродния моноксид от фигура 2 могат да се съставят двумерни образи, които да бъдат изобразени в равнината. Един от двата разумни начина е следният: първият признак е концентрацията на моноксида един час преди събитието, а вторият признак е концентрацията на моноксида в часа на събитието. Така от поредицата от 18 концентрации се съставят 17 двумерни образи, които са изобразени в двумерното пространство на фигура 5.
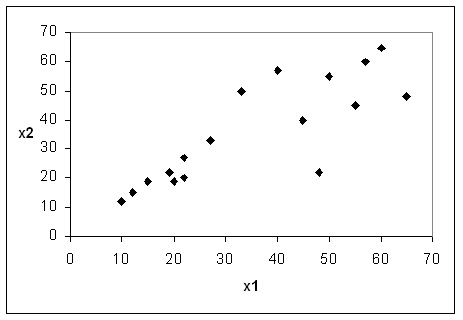
Фигура 5. Двумерното пространство на хемометричните образи, съставени от събитията от фигура 2.
4. Мерки за разстояние в пространството на образите. Ако признаците на хемометричния образ описват химичния обект (или събитие) химически състоятелно, то образите на подобни в химично отношетние обекти ще се намират близко в съответното пространство.
Образите от фигура 5 са изобразени в така нареченото Евклидово пространство, където мярката за разстояние, DE, се изчислява по позната формула (1), в която разстоянието е равно на корен квадратен от сумата от квадратите на разликите между съответните координати на образите X и W.
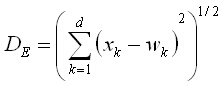 (1)
(1)
Разбира се, че могат да се дефинират и други мерки за разстояние. Една обща мярка за разстояние е разстоянието на Минковски, формула (2), в която M може да заема цели положителни числа – 1, 2, 3 и т.н.
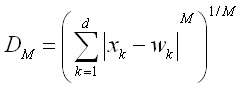 (2)
(2)
За M = 2 получаваме Евклидовото разстояние, а при M = 1 разстоянието се нарича разстояние в Манхатан (Manhatten distance или city block distance). На фигура 6 са дадени двете разстояния, Евклидовото е показано с удебелена линия, а това в Манхатън с две тънки линии, сумата от чиито дължини дава разстоянието.
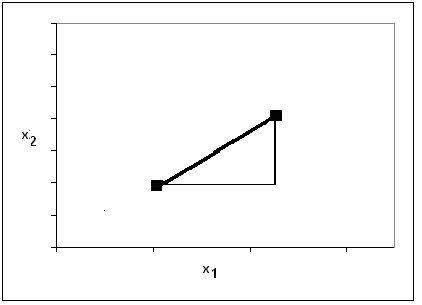
Фигура 6. Евклидово разстояние (удебелената линия) и разстояние в Манхатън (другите две линии) в двумерното пространство.
За образи, двоично кодирани с нула и единица се използват две други мерки за разстояние, разстояние по Хеминг (Hamming distance), формула (3) и разстояние по Танимото (Tanimoto distance), формула (4).
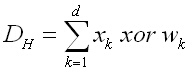 (3)
(3)
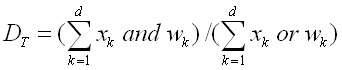 (4)
(4)
където xk и wk са к-тите координати на двоичните образи X и W, а функциите and, or и xor са съответните логически функции, чийто значения са дадени в таблица 1.
Таблица 1. Значение на логическите
функции and, or и xor.

На практика DT не представлява разстояние, а е мярка за подобие на двата образа, която заема своята максимална стойност единица при два еднакви образа X и W, и нула - при напълно различни образи. Една мярка за разстояние, която може да се направи от DT е 1 - DT.
Ако искате да затвърдите материала вижте теоретичните задачи. След това може да разгледате и една малка програма за представяне и търсене на двоични образи
Литература
[1] D.L. Massart, B.G.M. Vandeginste, S.N. Deming, Y. Michote, L. Kaufman; Chemometrics: A Textbook. Elsevier, Amsterdam, 1988.
[2] K. Varmuza; Chemometrics. Springer Verlag, Berlin, 1980.
[3] М. А. Шараф, Л. Иллмэн, Б.Р. Ковальски; Хемометрика. Химия, Ленинград, 1989 г.
[4] П. Джурс, Т. Айзенауэр; Распознавание образов в химии. Мир, Москва, 1977 г.
[5] J. Zupan, J. Gasteiger; Neural Networks for Chemist: An Introduction. VCH Publishers, Weincheim, Germany, 1993.
[6] В. Симеонов; Принципи на обработка на данни от химичните анализи. Изд. на СУ ”К. Охридски”, София, 1987, 1997 (второ издание)
[7] Васил Симеонов, Информационни
аспекти в химичния анализ. Изд. “Образователни технологии”, София,
1999.
Автор: Пламен Пенчев, Ph.D.
[ това е материал от брой 13 на списание "Коснос" www.kosnos.com]