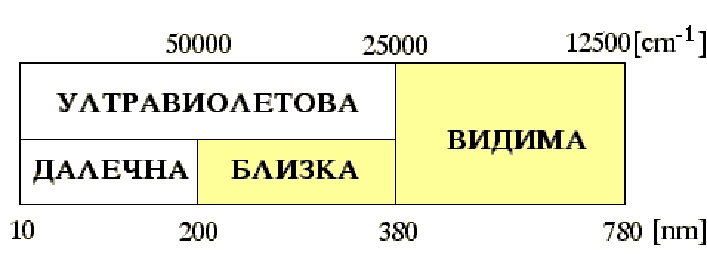
Преходите на валентни електрони между молекулни орбитали са свързани с поглъщане и излъчване на фотони от ултравиолетовата и видима област на електромагнитния спектър. Широко разпространени в практиката са спектрометрите, работещи в близката ултравиолетова и видима област - фигура 1.Електронна спектроскопия
Част 1
Електронни спектри на двуатомни молекули

В далечната ултравиолетова област поглъщат силно атмосферният азот и кислород, поради което спектрометрите работещи в нея трябва да бъдат евакуирани. Това е причина тази област да се нарича вакуумен ултравиолет.
Преразпределението на електронната плътност в молекулите при даден преход променя енергията на свързване между електроните и ядрата, което води до промени в енергията на трептене на атомите. Eлектронните преходи в дадена молекула са съпроводени с вибрационни преходи, които от своя страна имат фина ротационна структура, когато спектрите са регистрирани в газово състояние. Отделните вибрационни и ротационни линии в електронните спектри на вещества, измерени в кондензирана фаза, се сливат в широки ивици.
Чисто ротационни спектри ще се наблюдават
само при молекули, имащи постоянен електричен диполен момент. За поява
на вибрационни спектри е наложително диполният момент да се променя при
трептенето. За разлика от първите два случая електронни спектри се наблюдават
за всички молекули, тъй като преразпределението на електроните в молекулите
е винаги свързано с промяна на диполния момент. Това означава, че хомоядрените
молекули, като Н2, О2, Cl2 и др., които
нямат ротационни и вибрационно-ротационни спектри ще абсорбират ултравиолетова
или видима светлина. Нещо повече, електронните спектри на тези молекули,
регистрирани в газово състояние, имат фина вибрационно-ротационна структура,
от която могат да се получат редица молекулни параметри.
1. Електронни преходи в двуатомни молекули.
Пълната вътрешна енергия на една двуатомна молекула, Еtot, се дава с уравнението (1), където първите три члена са съответно електронната, вибрационната и ротационната енергия на молекулата, а последният е енергетичен член, който отчита взаимодействието между тях.
Еtot = EE + EV + ER + R (1)
Ако първоначално игнорираме ротационната енергия на преходите и члена R, (1) добива вида:
Еtot = EE + EV (2)
Ако заместим израза за вирационната енергия за анхармоничен осцилатор, EV, получаваме:
Еtot = EE + hn(v + 1/2) - xhn(v+ 1/2)2 (3)
където v =0,1,2.... се нарича вибрационно квантово число, а x е т.н. константа на анхармоничност, която е безразмерна и заема много малки положителни реални стойности (~0.01).
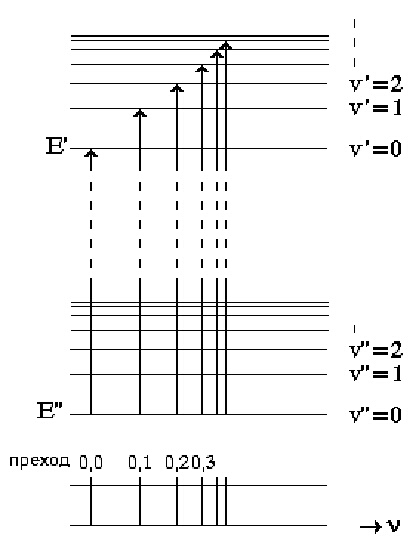
Енергетичните нива за две стойности на електронната енергия са изобразени схематично на фигура 2. Нека обърнем внимание, че разстоянията между вибрационните нива на възбуденото електронно състояние са по-малки от тези на съответните нива на основното електронно състояние. Това е в съответствие с отслабването на връзките между атомите във възбудено електронно състояние.
В електронната спектроскопия са по принцип възможни (с известна вероятност) всички преходи. На практика обаче не се наблюдават всички възможни, а предимно преходи от основното вибрационно на основното електронно състояние (фиг.2). Причина за това е обстоятелството, че почти всички молекули заселват при обикновена температура основните нива.
Отделните линии на електронния преход, дадени долу на фигура 2, се проявяват в спектъра като ивици, наречени v' прогресия, понеже стойността на v' нараства при всеки преход в поредицата, като отделните линии на ивицата се сгъстяват при високите честоти. Това е директно следствие от анхармоничността на трептенето в горното електронно състояние.
Аналитичният израз за честотата на погълнатия квант електромагнитно лъчение, nабс, при електронния преход може съгласно уравнение (3) да се запише по следния начин (тук на практика E'-E" е разликата между енергиите на електронните нива, а останалата част между вибрационните нива):
DЕtot = E' - E" + [hn(v'+1/2) - hn(v"+1/2)] - [xhn(v'+1/2)2 - xhn(v"+1/2)2] (4')
и
hnабс = DЕtot (4")
От (4) следва, че в електронния спектър може да се наблюдава поредица от вибрационни линии, въз основа на които се пресмята честотата на трептене и анхармоничността в основно и във възбудено състояние, както и разстоянието между двете състояния.
Подобен израз може да се запише и при отчитане на ротационния преход. Тогава в уравнение (4) се добавя и разликата B'j'(j'+1) - Bj"(j"+1), където B е ротационната константа на молекулата, а j" и j' са ротационните квантови числа на основното и възбуденото състояния.
Следователно, ако в електронния спектър на една двуатомна молекула се наблюдава фина структура, по нея могат да се определят ротационната константа, моментът на инерция и дължината на връзката на високото и по-ниско електронно състояние. Въз основа на данни от вибрационната структура на електронните ивици могат да бъдат пресметнати: честотата на трептене, силовата константа на връзката, а евентуално и енергията на дисоциация.
Най-съществената приложна страна на електронната
спектроскопия на двуатомни молекули е възможността за изследване на възбудени
състояния както и на свободни радикали. Изследването на промените в интензитета
за кратки периоди от време (импулсна фотолиза) дава информация за скоростта,
с която се образуват и разпадат радикалите.
2. Интензитет на ивиците в електронния спектър.
Интензитетите на вибрационните ивици на даден електронен преход при двуатомните молекули са различни, независимо от това, че всички преходи са разрешени. В някои от практически измерените спектри най-интензивен е преходът 0 а 0, в други - някоя друга ивица от прогресията. Има случаи, при които се наблюдават само няколко ивици, последвани от непрекъснат спектър. Тези три типа интензитети на електронните спектри се обясняват с принципа на Франк-Кондон, според който електронните преходи в молекулите се извършват така бързо в сравнение с вибрационните движения, че междуатомните разстояния остават практически непроменени през време на прехода, т.е. веднага след извършване на електронния преход, ядрата имат все още същото положение и скорост както преди прехода.
Анхармоничният осцилатор на двуатомна молекула може да се представи като един атом, трептящ спрямо другия, който се счита за неподвижен. Според класическите представи трептящият атом ще пребивава най-дълго време при възвратните точки на потенциалната крива, тъй като движението му там е най-бавно. Ако при преход на една двуатомна молекула от основно във възбудено електронно състояние тя остава стабилна, недисоциирана, то това възбудено състояние може да се представи с крива на потенциалната енергия, подобна на тази на основното състояние.
Има три възможности:
1. Равновесните разстояния между ядрата в основно и възбудено електронно състояние са еднакви. Тогава потенциалните функции са почти еднакви за двете състояния. Електронният преход ще се извършва от възвратната точка на ядрото на дадено вибрационно ниво от основното електронно състояние върху възвратната точка на дадено вибрационно ниво на възбуденото електронно сътояние. Следователно най-вероятен ще бъде преходът, за който вибрационните квантови числа са еднакви (т.н. вертикални преходи). В такъв случай най-интензивна ще бъде ивицата, съответствуваща на преход 0 а 0, а интензитетът на останалите ивици бързо ще намалява.
2. Ако междуатомното разстояние във възбуденото електронно състояние е малко по-голямо от това в основно, двете потенциални функции са (малко) отместени. Тогава вертикалният преход от v" = 0 към възбуденото електронно състояние може да се извърши до вибрационно състояние v' = 3, докато преходи до v' = 1 и 2 са по-малко вероятни. В резултат интензитетите на отделните електронно-вибрационни преходи ще бъдат както е показано на фигура 3 b).
3. Когато междуядреното разстояние във възбудено електронно състояние е значително по-голямо от това в основно, най-вероятен ще бъде преход към вибрационно ниво, при което енергията е по-голяма от дисоциационната енергия. В такива случаи се получава силно, непрекъснато поглъщане, отговарящо на дисоциация на молекулата, а всички дискретни преходи ще бъдат с по-нисък интензитет - фигура 3 c).
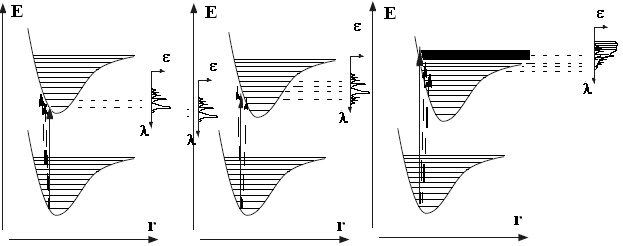
Фигура 3. Илюстрация на принципа на Франк-Кондон за формата на електронните абсорбционни ивици: a) междуатомните разстояния са еднакви за двете електронни състояния; b) междуатомните разстояния във възбудено състояние са малко по-големи от тези на основното; c) разликата в междуатомното разсояние е значителна. Най-лявата картинка е означена с a), средната - с b), а най-дясната е c).
Принципът на Франк-Кондон според квантовомеханичните
представи се модифицира по следния начин: преходът се извършва с предпочитание
от максимума на вероятността за пребиваване от едното електронно състояние
към максимума на вероятността за пребиваване в другото електронно състояние
- фигура 3 c. За v = 0 най-вероятно е равновесното положение, докато за
v = 1,2,3... максимум на вероятността се изместват встрани от центъра и
за големи стойности на v класическите и квантови представи дават един и
същи резултат.
3. Електронна структура на двуатомни молекули, форма на някои молекулни орбитали.
Атомните електрони притежават строго определена енергия и пространствено разпределение, които могат да се пресмятат с уравнението на Шрьодингер и да се изразяват като триизмерна вълнова функция j. Вълновата функция j, наречена още атомна орбитала, зависи от стойностите на трите квантови числа n, l и m. Спинът на електрона също има своя принос към енергията. Съществуват определени правила за заемане на атомните орбитали в основно състояние и възможните преходи между орбиталите.
Молекулните орбитали, означавани с Y, съгласно МО-теорията обхващат две или повече ядра. Формата и енергията на тези орбитали се пресмятат с уравнението на Шрьодингер. Тъй като подробните пресмятания са изключително трудни, се въвежда едно приближение, при което МО се разглеждат като суми и разлики от атомните орбитали (АО) на съответните атоми, т.н. линейна комбинация от атомни орбитали (ЛКАО).
Двуатомната молекула в ЛКАО-приближение се представя като образувана от две различни МО, чиито вълнови функции се дават по следния начин:
YBMO = j1 + j2 или YAMO = j1 - j2 (5)
където YBMO и YAMO са съответните свързваща (bonding molecular orbital) и антисвързваща (antibonding molecular orbital) орбитали, а j1 и j2 са атомни орбитали от атом 1 и атом 2.
Най-простият случай на молекула, водородната, се образува при припокриване на двата 1s орбитала на водородните атоми - фигура 4.
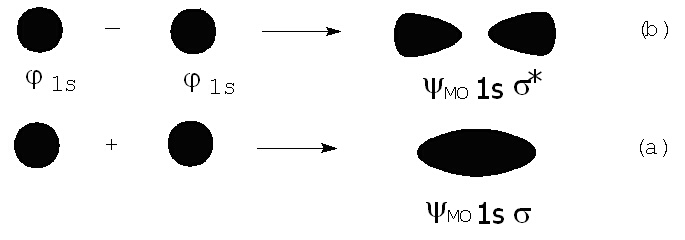
Това свързване може да се опише с молекулната орбиталите YBMO и YAMO (по традиция свързваща орбитала се отбелязва с 1ss, a антисвързващата - с 1ss*):
YBMO = j1s1 + j1s2 или YAMO = j1s1 - j1s2 (5)
Тъй като j1s1 и j1s2 са навсякъде положителни, в мястото на припокриване на атомните орбитали стойността на YBMO ще нарастне; формата на YBMO е симетричен елипсоид (виж фигура 4a). Концентрирането на електричен товар между ядрата ги свързва заедно, като по този начин се образува молекулна връзка. Затова тази орбитала се нарича свързваща 1ss (s-връзка, образувана от два 1s електрона).
За вълновата функция YAMO, получена съгласно втория израз в (5) в мястото на припокриване на двете атомни орбитали YAMO ще бъде нула, понеже близо до едното ядро вълновата функция ще бъде с положителн знак, а при другото - с отрицателен. Този случай е представен на фигура 4b. Формата на МО показва, че товарът е съсредоточен извън атомните ядра, което води до засилване на ядреното отблъскване. Тази молекулна орбитала има енергия по-висока от енергията на отделните атоми и се нарича антисвързваща; отбелязва се със звездичка - 1ss*. Всяка антисвързваща орбитала притежава възлова равнина (повърхнина, на която стойността на вълновата функция е нула).
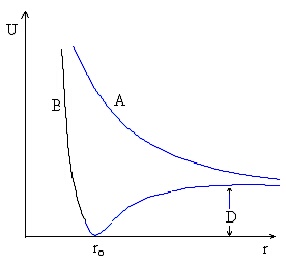
Енергията на взаимодействие между водородните атоми, U, е функция на междуядреното разстояние. Свързващата молекулна орбитала има минимум при равновесното разстояние r0, а антисвързващата съответствува на неустойчива конфигурация, при която енергията намалява непрекъснато с нарастване на r - това е изобразено на фигура 5.
Припокриването на две 2s-атомни орбитали води до образуване на свързваща 2ss и антисвързваща 2ss* молекулни орбитали, които имат форми, съответно идентични на 1ss и 1ss*, но са по-големи по размер и са с по-висока енергия.
При разглежданите два случая, свързващите молекулни вълнови функции запазват знака си при операцията на симетрия инверсия спрямо центъра на симетрия, който център притежава водородната молекула (виж статиите за симетрия в списанието). Затова тези свързващи молекулни орбитали се бележат със символа "g" (от немската дума четен - gerade) -- 1ssg и 2ssg. Антисиметричните вълнови функции се бележат с "u" (от немската дума нечетен - ungerade) -- 1ss*u и 2ss*u, защото променят знака си при инверсия в центъра на симетрия на молекулата.
Припокриването на две 2p-атомни орбитали може да се извърши по два различни начина за образуване на МО. Когато двете 2р орбитали лежат по оста Х (която ос е по връзката в двуатомната молекула), получените две молекулни вълнови функции се изразяват аналогично на уравнения (5):
YBMO = j2p1 + j2p2 или YAMO = j2p1 - j2p2 (6)
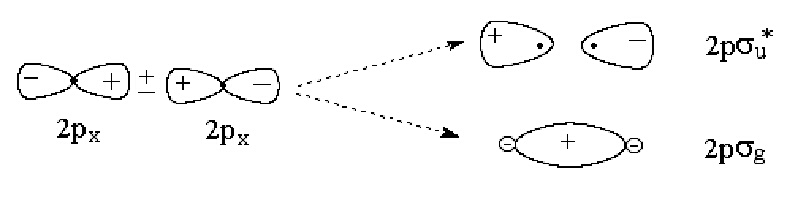
Свързващата молекулна орбитала 2psg и антисвързващата 2ps*u имат представената на фигура 6 форма.
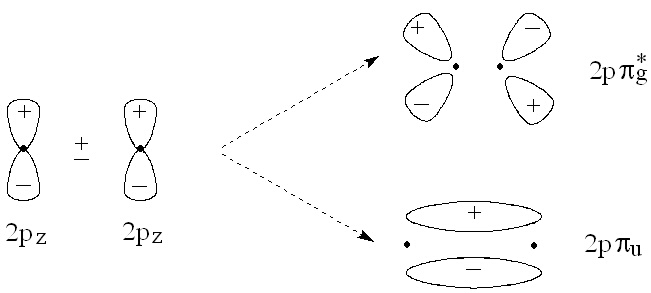
Когато двете атомни 2р орбитали са разположени по оста Z (която е перпендукулярна на връзката в двуатомната молекула), тяхното припокриване води до съсредоточаване на електроните в две области - над и под ядрата. Получените две молекулни орбитали се наричат p-орбитали. Свързващата орбитала е нечетна и се означава като 2ppu, докато антисвързващата е четна (симетрична спрямо инверсния център) и се бележи с 2pp*g - фигура 7.
При образуване на молекулни орбитали от атомни орбитали, принадлежащи на различни атоми, се запазват същите закономерности с тази само разлика, че участието на различните атомни орбитали е различно. По-електроотрицателният от атомите участвува в по-голяма степен в свързващата молекулна орбитала, докато по-слабо електроотрицателният - в по-голяма степен в антисвързващата.
Свързващи и съответно антисвързващи p-орбитали могат да се образуват и при припокриване на хибридни атомни орбитали с други хибридни, а също и хибридни орбитали с s- и p-електронни атомни орбитали.
Свободните електронни двойки от даден хетероатом, които не участвуват в образуване на молекулната орбитала, остават в силовото поле на атомите; енергията им на свързване не се променя поради участие на атома в съответната МО. Ето защо тези свободни електронни двойки, наречени n-електрони, заемат орбитали, енергията на които е равна на енергията на атомните електрони преди образуване на МО: тези орбитали се наричат несвързващи (nonbonding orbitals).
Литература
1. Г. Андреев. Молекулна спектроскопия, Изд. ПУ “П. Хилендарски”, Пловдив, 1999.
Автор: Проф. дхн Георги Андреев