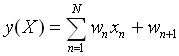от лекцията е уравнение на права с коефициенти
пред съответните координати, ak
= wk,
и свободен член b = wk+1.
Задачи
по материала
Класификация
по разстоянието до центроидите на класовете
X1 = (0.7, 0.2, 0.1, 0.8) X2 = (0.6, 0.1, 0.2, 0.5)
a) Изчислете сумата им S = X1 + X2
b) Изчислете разликата им D = X1 - X2
c) Изчислете произведението на първия с числото 0.4: P = 0.4 X1
Вижте решението на задачата.
Задача T2. Имате пет четиримерни образа:
X1
= (0.7, 0.2,-0.1,-0.8)
X2
= (0.6, 0.1, 0.2, 0.5)
X3
= (0.7,-0.6, 0.3, 0.8)
X4
= (0.5, 0.5, 0.4, 0.5)
X5
= (0.3, 0.4, 0.4, 0.5)
Изчислете образа, който отговаря на центроида на тази извадка M.
Вижте решението на задачата.
Задача T3. Имате два четиримерни образа:
X1
= (0.7, 0.2, 0.1,-0.8)
X2
= (0.6, 0.1, 0.2, 0.5)
Изчислете разстоянието в Манхатан от тях до центроида от предната задача M.
Вижте решението на задачата.
Задача Т4. От лекциите по Аналитична геометрия си припомнете уравнението за равнина в тримерното пространство. Обобщете уравнението за случая на N-мерно пространство. Намирате ли прилика с уравнение (1) от лекцията? Ако да, за коя равнина става въпрос в уравнение (1)?
Вижте решението на задачата.
Задача Т5. Пречи ли на класификацията припокриването на образите от двата класа в пространството на образите? Как влияят бегълците (outlayers) на положението на центроидите? А на класификацията?
Вижте решението на задачата.
ЛИТЕРАТУРА
[1] K. Varmuza; Chemometrics. Springer Verlag, Berlin, 1980.
[ това е материал от брой 16 на списание "Коснос" www.kosnos.com ]
a) Сумата им е
S = (0.7 + 0.6, 0.2 + 0.1, 0.1 + 0.2, 0.8 + 0.5) =
= (1.3, 0.3, 0.3, 1.3)
b) Разликата им е
D = (0.7 - 0.6, 0.2 - 0.1, 0.1 - 0.2, 0.8 - 0.5) =
= (0.1, 0.1, -0.1, 0.3)
c) Произведението 0.4 X1 е
P = (0.4x0.7, 0.4x0.2, 0.4x0.1, 0.4x0.8) =
= (0.28, 0.08, 0.04, 0.32)
За да намерим центроида M на тази извадка първо събираме тези пет четиримерни образа (образите като векторите се събират като се събират съответните им координати):
X1
= (0.7, 0.2,-0.1,-0.8)
X2
= (0.6, 0.1, 0.2, 0.5)
X3
= (0.7,-0.6, 0.3, 0.8)
X4
= (0.5, 0.5, 0.4, 0.5)
X5
= (0.3, 0.4, 0.4, 0.5)
-------------------------
S = (2.8, 0.6, 1.2, 1.5)
След това разделяме сумата на броя на образите - случая 5. Образите като векторите се делят на число като се делят съответните координати на числото.
M = S / 5 =
= (2.8 / 5, 0.6 / 5, 1.2 / 5, 1.5 / 5) =
= (0.56, 0.12, 0.24, 0.30)
Разстоянието от X1 до центроида M от предната задача е:
D1 = |0.7 - 0.56| + |0.2 - 0.12| + |0.1 - 0.24| + |-0.8 - 0.30| =
= 0.14 + 0.08 + 0.14 + 1.10 =
= 1.46
Аналогично, разстоянието от X2 до центроида M от предната задача е:
D1 = |0.6 - 0.56| + |0.1 - 0.12| + |0.2 - 0.24| + |0.5 - 0.30| =
= 0.04 + 0.02 + 0.04 + 0.2 =
= 0.3
Т.е. образ X2 е по-близко до центроида M, отколкото X1.
Уравнението на равнина в тримерното пространство е следното: a x + b y + c z + d = 0. За N-мерно пространство с координати (оси) x1, x2, x3, ... и xN уравнението на една хиперравнина ще бъде
a1 x1 + a2 x2 + a3 x3 +... + aN xN + b = 0
Фактически уравнение 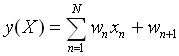(1)
от лекцията е уравнение на права с коефициенти
пред съответните координати, ak
= wk,
и свободен член b = wk+1.
Припокриването на образите не пречи на класификацията, защото разделящата равнина се определя от центроидите, а не от част от образите. Разделящата равнина минава през центъра на отсечката, която свързва двата центроида, и е перпендикулярна на нея - вижте фигура 2 в лекцията.
Бегълците, т.е. данните, които са встрани от повечето образи от техния клас, съвсем слабо влияят на положението на центроидите (защото последните са средни стойности от всички обекти). Съответно, те съвсем слабо влияят и на класификацията. Това е едно от основните предимства на този метод.
[ това е материал от брой 16 на списание "Коснос" www.kosnos.com ]