Вибрационна спектроскопия
част 2
В предишния
материал се запознахме с хармоничния осцилатор, който бе разгледан
в класическо и квантово-механично приближение. В този материал ще се запознаем
с анхармоничния осцилатор и ротационната структура на един вибрационен
преход.
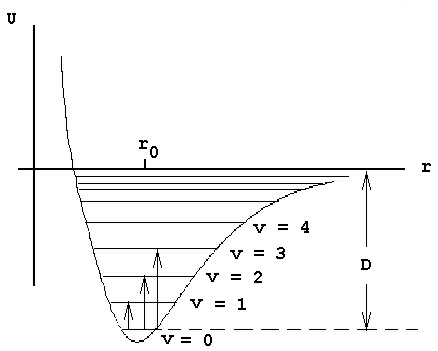
1. Анхармоничен осцилатор. Трептенията на двуатомните молекули се извършват със значителни амплитуди, поради което те представляват в действителност анхармонични осцилатори. В такъв случай, в израза за потенциална енергия (11) от предишния материал, трябва да бъде включен и кубичният член (а евентуално и членовете от по-висок порядък). Тогава потенциалната крива на анхармоничния осцилатор, съответно на реална двуатомна молекула, се променя. Тя ще има форма близка до парабола само в близката околност на r = r0. При намаляване на r функцията става по-стръмна от парабола, а при увеличаване на r става по-полегата и клони асимптотично към една постоянна стойност, съответствуваща на дисоциационната енергия на химичната връзка - фигура 1.

Фигура 1. Потенциална функция, енергетични нива и преходи при анхармоничен осцилатор.
Потенциалната енергия на анхармоничния осцилатор може да се представи с различни приближени функции (Морзе, Бъкингам, Ленард-Джонс) най-известната от които е тази на Морзе:
![]() (1)
(1)
Анализът на функцията на Морзе показва, че:
1. при r = r0, a(r - r0) = 0, следователно U(r0) = 0;
2. при r < r0 или r > r0 U(r) е положителна;
3. при r клонящо към минус безкрайност, -a(r -r0) клони към плюс безкрайност и следователно U(r) клони към плюс безкрайност: това съответства на силите на отблъскване при приближаване на ядрата;
4. при r клонящо към плюс безкрайност, -a(r -r0) клони към минус безкрайност и следователно U(r) клони асимтотично към De.
Разлагането на функцияна на Морзе в ред води до следнота приближена зависимост на U от r-r0:
U(r) = а2De(r - r0)2 (2)
Вземайки под внимание (11) от предишния материал за силовата константа к получаваме:
k = 2а2De (3)
Последното уравнение дава възможност да се свържат химичните свойства на двуатомната молекула (нейната енергия на дисоциация De) с честотата на трептене на атомите, която от своя страна пряко зависи от k.
Въвеждането на допълнителен член в потенциалната функция, отчитащ анхармоничността, води до промяна и на квантово-механичния израз за енергията:
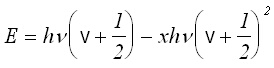 (4)
(4)
където х е т.н. константа за анхармоничност, имаща стойност по-малка от 1, х е около10-2.
Вибрационното квантово число v в (4) може да заема всички цели неотрицателни стойности, както и в случая на хармоничния осцилатор:
v = 0, 1, 2, 3 . . .
Анхармоничността е причина за промяна на подборните правила; в този случай стават разрешени преходи между кои да са две нива, т.е.
Dv = ±1, ± 2... (5),
обаче вероятността за преход намалява рязко с нарастване на v.
От (4) следва, че с нарастване на вибрационното квантово число v разстоянията между енергетичните нива ще намаляват, т.е. нивата постепенно се сближават и накрая се сливат, давайки непрекъснат спектър - вижте фигура 1.
От фигура 1 се вижда, че спектърът на анхармоничния осцилатор ще представлява система от ивици, най-нискочестотната от които се нарича основен тон (преход v=0 аv=1), следващата - първи обертон (преход преход v=0 аv=2), втори обертон (преход преход v=0 аv=3) и т.н. до непрекъснат спектър. Поради системно сближаване на нивата, първият, вторият и т.н. обертонове не притежават честоти, точно кратни на тази на основната (съответно 2n0, 3n0 и т.н.), а малко по-ниски.
2. Вибрационно-ротационен спектър. Съгласно приближението на Борн-Опенхаймер, енергиите на трептене и на въртене могат да се считат за независими. Ротационните линии на двуатомните молекули са разположени в микровълновата област, най-често около 10 cm-1, докато честотите на трептене - около 3000 cm-1. В такъв случай, пренебрегвайки взаимодействието между трептене и въртене и приемайки, че енергията на трептящия ротатор ЕT е сума от анхармоничния осцилатор и нетвърдия ротатор се получава:
ЕT = ЕV + ЕR (6)
За съответния вибрационно-ротационен терм Т, може съгласно (2.1) и (3.17), да се запише:
Т = G(V)+F(j)=(v+1/2)-x(v+1/2)2+Bj(j+1)-Dj2(j+1)2 (7)
Правилата за подбор при съвместното вибрационно-ротационно движение са същите, както за всяко от тях поотделно, т.е.
Dv= ±1, ±2...; Dj= ±1
С други думи, един вибрационен преход е свързан с едновременна промяна и на ротационните състояния.
Честотата на чисто вибрационния терм `n0, съответствуваща на прехода v' а v" се дава с израза:
![]() (8)
(8)
Добавяйки ротационния терм, за честотата на вибрационно-ротационния преход се получава:
n = n0 + B'j'(j'+1)-B"j"(j"+1) + D"j"2(j"+1)2-D'j'2(j'+1)2 (9)
При абсорбционните преходи Dj=+1, т.е. j'=j"+1. Съгласно (9) се получава:
n = n0 + B'(j"+1)(j"+2)-B"j"(j"+1)+D"j"2(j"+1)2-D'(j"+1)2(j"+2)2 (10)
Пренебрегвайки поправката за нееластичен ротатор (т.е. при D'=0 и D"=0), уравнение (10) може да се запише:
n = n0 + B'(j"+1)(j"+2)-B"j"(j"+1)
Ако приемем, че ротационната константа В е еднаква за горното (v') и долно вибрационно ниво (v"), т.е B' = B" = B, то получаваме
nR = n0 + 2B(j"+1) (11)
Вълновото число на прехода го означихме с nR за да се прави разлика от емисионния преход, където то се означава с nP.
Правейки същите разглеждания за честотата на вибрационно-ротационния преход, при който j'=j" - 1, т.е. при емисионен преход, се получава:
nP = n0 - 2B(j"+1) (12)
Формулите (11) и (12) описват две серии от линии, чиито преходи са представени на фигура 2.
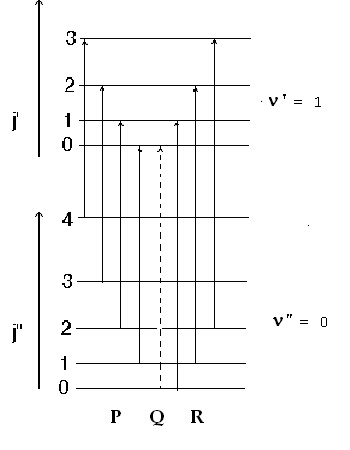
Преходите, свързани с нарастване на ротационното квантово число j,Dj = +1, образуват т.н. R-клон на вибрационно-ротационни ивици, а тези с намаление на j (Dj = -1) съставят Р-клона. Чистият вибрационен преход, който не е свързан с промяна на ротационното квантово число (Dj = 0), наречен Q-клон, е забранен - пунктирна стрелка на фигура 2.
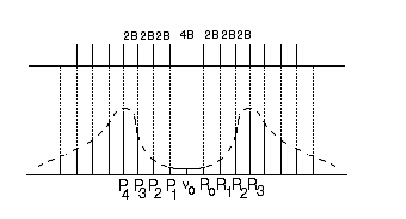
Ротационните линии на фигура 2 са изобразени на еднакво разстояние една от друга. В експериментално измерваните вибрационно-ротационни спектри на двуатомните молекули се наблюдава сближаване (сгъстяване) на линиите в R-клона и раздалечаване в Р-клона с нарастване на j - вижте фигура 3. Причина за това е взаимодействието между двете движения, трептеливо и въртеливо, поради което разликата между ротационните константи В' и B" е значителна (В' < B").
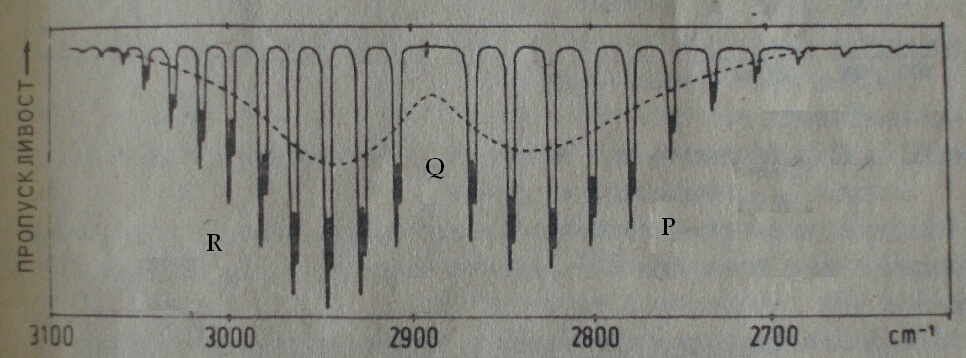
Фигура 3. Вибрационно-ротационен спектър на HCl. Ивиците от R-клона се сближават, а тези от P-клона се раздалечават. Причина за разцепване на всяка от ивиците е изотопният ефект на хлорния атом в H35Cl - H37Cl.
Въз основа на данни от вибрационно-ротационните спектри на двуатомни молекули може да се пресметнат константите В' и B", а оттам и междуатомното разстояние в основно и възбудено вибрационно състояние.
Спектърът на HCl, представен на фигура 3, е измерен на спектрометър със средна разделителна способност. Регистрирането на отделните линии на ротационно-вибрационни преходи на такъв спектрометър е възможно само при изследване на малки молекули с ниски инерчни моменти. При многоатомните молекули отделните ротационни линии на вибрационния спектър се припокриват и дават един общ ивичен контур.
Квантовомеханичните подборни правила за промяна на ротационната енергия при даден вибрационно-ротационен преход показват каква е симетрията на чистия вибрационен преход. Типът на симетрия, към който принадлежи последният, ще определи кой преход между ротационни нива на изходното и крайно вибрационно ниво ще бъдат разрешени. Това обстоятелство е причина за поява на еднакви ивични контури при вибрационно-ротационни преходи с еднаква симетрия. Ако всички нормални трептения на дадено съединение са активни в инфрачервения спектър, то за трептенията с различна симетрия ще се наблюдават различни ивични контури. Обратно - формата на контура може да се използува за определяне симетрията на преходите на молекули в газообразно състояние.
Типични ивични контури на вибрационно-ротационни спектри са показани на фигура 4.
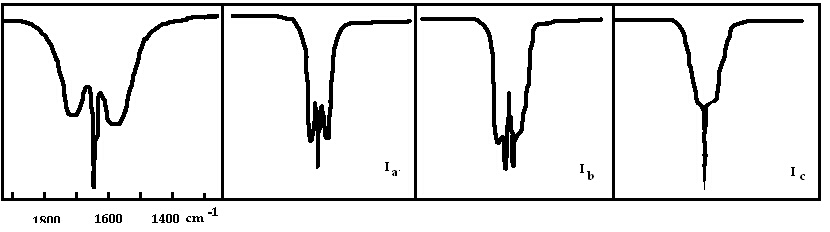
Фигура 4. Ивични контури във вибрационно-ротационни спектри на: а/ симетричен ротатор (NH3); б/ асиметричен ротатор (ивици за вибрационно-ротационни преходи в посока на главните инерчни моменти Ia, Ib и Ic).
Литература
1. Г. Андреев. Молекулна спектроскопия, Изд. ПУ “П. Хилендарски”, Пловдив, 1999.
Автор: Проф. дхн Георги Андреев