 (1)
(1)
Обучаващата машина може да бъде дефинирана като “устройство, чиито действия са повлияни от миналия опит” [1]. Линейната обучаваща машина (ЛОМ, на английски linear learning machine) е стравнително прост алгоритъм, който се побира в тази дефиниция, и който алгоритъм няма нищо общо с обучението, което претърпяват живите интелигентни организми.
В най-разпространените химически приложения ЛОМ представлява съвкупността от един N-мерен вектор W и правилата за промяната на неговите координати wn, наречени тегла [1,2]. Тази промяна се нарича обучение и се осъществява с помощта на обучаваща извадка, в която образите (обектите) са предварително разпределени в класове. Всеки образ от обучаващата извадка се пропуска като вход в ЛОМ и се определя неговото класово разпределение: при грешно такова се извършва корекция на коефициентите на обучаващия вектор и обучението продължава със следващите образи. То спира при достигане на 100% разпознавателна способност или някакъв брой предварително определени преминавания през цялата обучителна извадка: едно преминаване се нарича цикъл, сесия или епоха (session, epoch). Резултатите от това обучение могат да се проверят с помощта на тестваща извадка, с която може да се изчисли така наречената предсказваща способност (prediction ability)– това е процентът на правилно класифицираните образи от обучаващата извадка: тук задължително се предполага, че това са различни образи от образите в обучаващата извадка. Съответно тази статистика за обучаващата извадка се нарича разпознаваща способност (recognition ability) - за по-подробни сведения за обучението в хемометриката и различните извадки вижте този материал.
Чрез поредица от двоични класификации ЛОМ може да се използва при мултикласификационни проблеми, но реално алгоритъмът за обучение е за разделяне на образите в два класа. За извършване на това обучение всички налични N-мерни образи с известни класове се превръщат в (N+1)-мерни като се прибавя (N+1) координата към тях, чиято стойност е еднаква за всички образи. След това те се разпределят случайно между двете извадки – обучаващата и тестващата. Обучаващата извадка се “разбърква”, т.е. обучението на ЛОМ се осъществява в случаен ред на срещане на различните образи, а не, например, първо с образите от единия клас, а после с тези от другия.
Нека за двата класа, 0 и 1, поставим следните изисквания за големината на скаларното произведение между тегловния вектор W и съответния образ Xk.
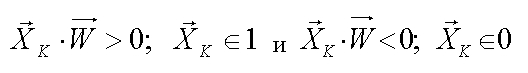 (1)
(1)
Нека в процеса на обучение за даден образ се получава грешно скаларно произведение
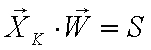 (2)
(2)т.е. ако обектът е от клас 1, S < 0, или ако обектът е от клас 0, то S > 0, което е точно обратното на изискванията в уравнение (1). Тогава корекцията на координатите на тегловния вектор W са следните (с прим е означен новият тегловен вектор):
![]() (3)
(3)
Като искаме така да променим тегловния вектор, че скаралното произведение да промени своята стойност в точно противоположната:
![]() (4)
(4)
Замествайки уравнения (2) и (3) в уравнение (4) получаваме
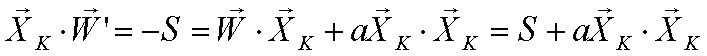
или
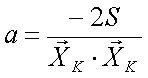 (5)
(5)
Обучението започва със случайни стойности на тегловния вектор W. В литературата ([2] и цитатите там) са описани изследвания с начални стойности Wn между -1 и +1, както и обучения, стартирали при всички координати на W, равни на единица или всички, равни на минус единица.
Векторът W определя една хиперравнина в (N+1)-мерното пространство, която има уравнение
![]() (6)
(6)
което показва, че тази хиперравнина минава през началото на координатната система.
W
е перпендикулярен на тази равнина. На фигура 1 е показана тази равнина
в тримерното пространство – образите са двумерни, но както бе споменато
по-горе, към тях е прибавена трета координата с една и съща стойност, която
ги отмества в равнина, успоредна на равнината xOy. На фигурата е показан
нормалният вектор n към равни-ната – при нашите изисквания от уравнение
(1), векторът W ще сочи в обратна посока на n. Освен това не е необходимо
дължината на W да е единица, както е дължината на n. От фигурата се вижда
и необходимостта да се добави допълнителна (в случая трета) координата
– тя довежда до това, че разделящата равнина минава през началото на координатната
система и затова могат да се формулират условията в уравнения (1) по този
начин; вижда се, че правата която е сечение между двете равнини и която
на практика разделя образите от двата класа не минава в общия случай през
началото на координатната система (в двумерното пространство в този конкретен
случай).
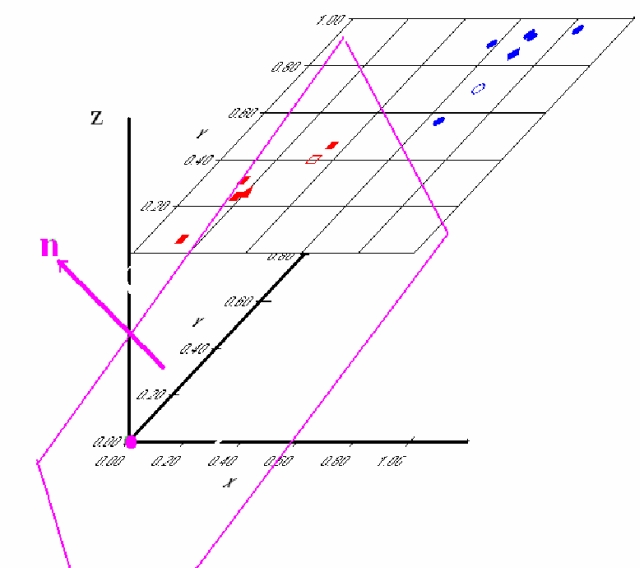 |
... | Фигура 1. Разделящата равнина, която се получава при пълно обучение на девет образа от два класа. Тези от клас 0 са означени с квадрати, тези от клас 1 – с кръгове, техните центроиди, съответно с триъгълник и ромб, а двата непознати образа с празен квадрат и празен кръг. |
Както споменахме обучението, т.е. корекцията по уравнение (3) се извършва само за образите, които дават “неправилно” скаларно произведение. За образите, които се класифицират правилно съобразно изискванията в уравнения (1) не се извършват корекции. Ако при едно пълно преминаване през обучаващата извадка няма нужда от нито една корекция, то обучението е завършено. На практика това става, т.е. алгоритъмът е сходим за линейно разделени образи (такива образи, между които може да се прекара разделяща равнина, при което образите от единия клас са от едната и страна, а тези от другия от друга и страна). Ако образите са линейно неразделими обучението се спира след предварително зададен брой сесии (епохи, цикли). В този случай е очевидно, че разпознаващата способност ще е различна от 100%, и тъй като предсказващата способност е винаги по-малка от нея, то и тя ще е по-малка от 100%.
Практически задачи
Задача C1. Отворете файла llm.xls. Разгледайте таблицата (sheet) Spectra, в която са дадени девет двумерни образа от два класа. В таблицата LLM двумерните образи са превърнати в тримерни, разбъркани са, и е извършено обучение с начални стойности на координатите на w, равни на 1.0.
В таблицата WORK извършете обучение, като използвате начален вектор W = (-1.0, 1.0, -1.0).
Упътване:
В таблицата (sheet) Spectra са дадени девет двумерни образи, които са разделени на два класа, 0 и 1, които са първични алкохоли (образи 5 - 9, клас 1) и съединения, които нямат групата -CH2OH, клас 0. Първият признак е максимумът на абсорбцията на ИЧ лъчение в интервала 3578 - 3278 cm-1 (клетки C2:C10) , а вторият - максимумът на абсорбцията на ИЧ лъчение в интервала 1079 - 1003 cm-1 (клетки C2:C10). В редове 11 и 12 са изчислени и съответните центроиди на двата класа (за справка що е това вижте този материал). В дясно е дадена двумерна графика, която показва деветте образа, двата центроида и образите на двете неизвестни съединения, X0 и X1.
В таблицата (sheet) LLM на същия файл е проведено обучение с тези девет образа. За целта образите са разбъркани и е добавена трета координата в клетки F2:F10, която има една и съща стойност, равна на единица. В клетки G2:G10 са изчислени квадратите на големините на деветте (вече тримерни) образа, които големини са необходими за корекциите, в които се използва константата a от уравнение (5).
Трите начални координати на вектора W са дадени в клетки D17:F17. Скаларното произведение на този начален вектор и първия от разбърканите образи е изчислено в клетка C18 и е равно на 1.19, стойност, която е положителна, а образът е от клас 0, което изисква то да е отрицателно. Необходимите корекции на вектора W са изчислени по формула (2) в клетки D19:F19.
Задача C2. В таблицата (sheet) DataPlot на същия файл е начертана разделящата права, която съответства на разделящата равнина, определена от вектора W4. Това е тегловният вектор, получен при обучението от таблицата LLM. Тази права се получава по следния начин:
Уравнението на обучаващата равнина е следното
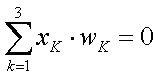
където xk са координатите в тримерното пространство (вместо x, y и z). Тъй като третата координата на всички образи бе направена равна на единица, т.е.x3 = 1, то това уравнение е:
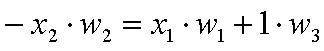
или записано спрямо x2:
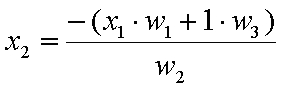 (7)
(7)
Което уравнение се изполва за изчисляване на стойностите на x2 в клетки B21:B31.
Копирайте координатите на получения от задача C1 тегловен вектор в клетки C17:E17, и в клетка C21 напишете формулата =-(A21*$C$17 + $E$17)/$D$17, която ще приложи уравнение (7) за изчисления от вас в предната задача тегловен вектор. Разпънете тази формула от клетка C21 до C31 и добавете нова права във фигурата. Добавянето на нова права се извършва с менюто Chart | Add Data. Ако имате проблеми изберете новите точки и горе в полето за формула напишете =SERIES(,DataPlotNew!$A$21:$A$31,DataPlotNew!$C$21:$C$31,3)
С десния клавиш на мишката извикайте локално меню е направете точките на права.
Задача C3. В таблиците (sheet) DataPlot на същия файл
[1] K. Varmuza; Chemometrics. Springer Verlag, Berlin, 1980.
[2] П. Джурс, Т. Айзенауэр; Распознавание
образов в химии. Мир, Москва, 1977.
..
Автор: Пламен
Пенчев, Ph.D.
[ това е материал от брой 22 от август 2008 г. на списание "Коснос" www.kosnos.com ]