С предишния материал започнахме една поредица за приложение на статистиката в химията. Материалът може да се използва не само от химици, а от всички, които се занимават с обработка на експериментални резултати. В тази лекция ще разгледаме някои статистически разпределения.
1. Равномерно разпределение. Това е такова разпределение, за което плътността на вероятността р(Х) е постоянна и различна от нула в даден интервал и равна на нула извън него.
м С
за а <= Х <= b
р(Х) = н
о
0 за Х < а и b > Х
Вероятността случайната величина да заема
стойности в интервала (-![]() , +
, +![]() )
е единица,
)
е единица,
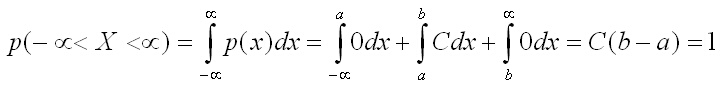
като първият и третият интеграл са нули поради равенство на подинтегралната функция на нула. При интегрирането се получава
С(b - а) = 1, т.е.С = 1/(b - а).
 |
... |
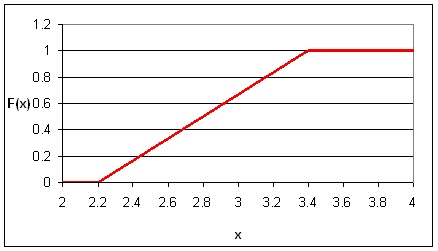 |
Функцията на разпределение е интеграл от плътността на вероятността и е равна на:
м 0,
за Х < а
F(Х) = н
(X - a)/(b - а), за а
<= Х <= b
о 1,
за Х > b
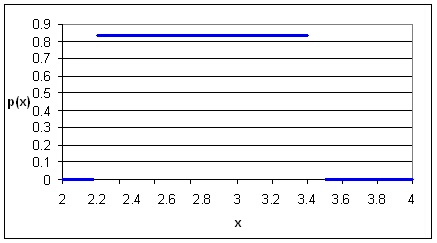
На фигури 1.6. и 1.7. са изобразени двете функции р(Х) и F(Х).
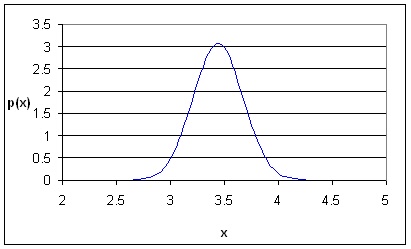
2. Нормално разпределение. Непрекъсната случайна величина е разпределена нормално и тя се нарича нормална, ако плътността и на разпределение има вида:
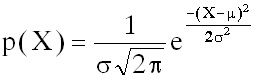 (1.5)
(1.5)
 |
... | 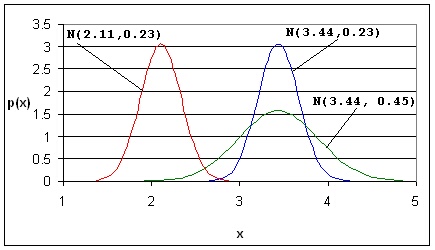
Фигура 1.9. Плътност на нормалото разпределение за различни стойности на m и s; m = 2.11 и s = 0.23; m = 3.44 и s = 0.23; m = 3.44 и s = 0.45. |
Другото име на това разпределение е Гаусово
разпределение. Дадено нормално разпределение се означава със записа
N(m,s),
където m
и s
са така наречените параметри на разпределението. Графичният вид на тази
функция (вижте фигура 1.8) е камбановидна крива, симетрична относно правата
Х
= m,
с максимум за Х = m
и с инфлексни точки за Х = m
- s
и Х = m
+ s.
При Х = m
+ 3s
нейната стойност е почти нула в сравнение с максимума: р(Х)
= 0.011р(m).
Коефициентът пред експонента осигурява нормираността на плътността на разпределението,
т.е. вероятността за намиране на случайната
величина в интервала (-![]() , +
, +![]() )
е единица (вижте задача 1):
)
е единица (вижте задача 1):
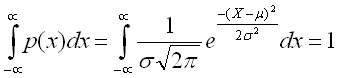
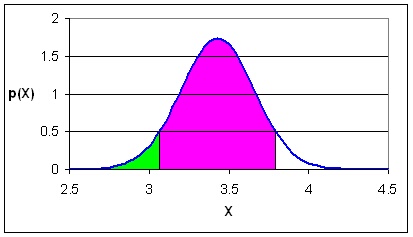
Промяната на стойността на m измества кривата по координата Х без да променя наклона и, а изменението на s променя само нейния наклон. При по-големи стойности на s кривата е по-полегата и с по-нисък максимум, вижте фигура 1.9.
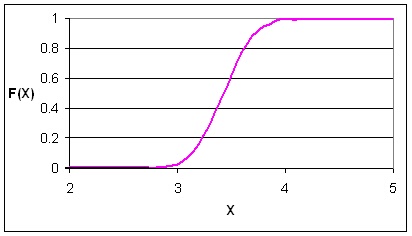
Функцията на разпределение се дава с интеграла,
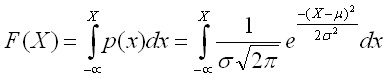
който се нарича интеграл на Лаплас
и е нерешим в явен вид. Графичният вид на тази функция е представен на
фигура 1.10. Математическото очакване на нормалното разпределение е равно
на m,
а дисперсията на s2
- вижте задача 2 и нейното решение.
 |
... |
 |
Ако в (1.5) се смени променливата Х с У=(Х-m)/s, се получава нормирано нормално разпределение или така нареченото стандартно разпределение. То има следната плътност на разпределение:
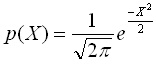
Според формула (1.4) от предишния материал математическото очакване и дисперсията на стандартното разпределение са съответно 0 и 1 - вижте също и задача 2.
Както видяхме стандартното разпределение
е нормално разпределение с параметри m=0
и s2=1.
В приложение 1
са дадени числените решения
F(Х)
на интеграла на Лаплас за стандартното разпределение в граници от -![]() до X.
Често е необходимо намирането на негово решение F'(Х)
в граници от -X
до +X.
Между двете стойности съществува връзката F'(Х)=2F(Х)-1,
която е следствие от симетричността на плътността на разпределение, вижте
фигура 1.11. Двата интеграла от приложението F'(Х)
и F(Х)
могат да се използуват за произволно нормално разпределение, като е необходимо
границите на интегриране за последното да са изразени в единици s.
Например за m =
3.44 и s
=
0.23 границата на интегриране 4.00
в единици s
е равна на (4.00-3.44)/0.23=2.44.
до X.
Често е необходимо намирането на негово решение F'(Х)
в граници от -X
до +X.
Между двете стойности съществува връзката F'(Х)=2F(Х)-1,
която е следствие от симетричността на плътността на разпределение, вижте
фигура 1.11. Двата интеграла от приложението F'(Х)
и F(Х)
могат да се използуват за произволно нормално разпределение, като е необходимо
границите на интегриране за последното да са изразени в единици s.
Например за m =
3.44 и s
=
0.23 границата на интегриране 4.00
в единици s
е равна на (4.00-3.44)/0.23=2.44.
Задача 1. Вероятността
случайната величина да заема стойности в интервала (-![]() ,
+
,
+![]() ) е единица. Докажете това
за нормалното разпределение - съответният интеграл няма решение, но двойният
интеграл по-долу може да се реши със замяна на променливите x
и y
с радиални координати r
и q.
) е единица. Докажете това
за нормалното разпределение - съответният интеграл няма решение, но двойният
интеграл по-долу може да се реши със замяна на променливите x
и y
с радиални координати r
и q.
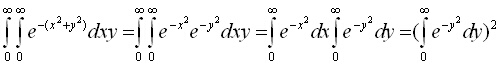
Вижте решението на задачата.
Задача 2. Намерете
математическото очакване и дисперсията на равномерното разпределение.
Вижте решението
на задачата.
Задача 3. Докажете,
че математическото очакване и дисперсията на нормалното разпределение са
съответно m
и s2.
Вижте решението
на задачата.
Задача 4. За
стандартното разпределение докажете, че F'(Х)
= 2F(Х) - 1, където F(Х)
е интеграл в граници от -![]() до X,
а F'(Х)
- интеграл в граници от -X
до +X.
Използвате симетричността на Гаусовата крива.
до X,
а F'(Х)
- интеграл в граници от -X
до +X.
Използвате симетричността на Гаусовата крива.
Вижте решението
на задачата.
Задача 5. За стандартното разпределение
намерете от приложение
1 F'(2.87)
и F(2.87),
където F(2.87)
е интеграл в граници от -![]() до 2.87,
а F'(2.87)
- интеграл в граници от -2.87
до +2.87.
Използвайте, че F'(Х) = 2F(Х)
- 1.
до 2.87,
а F'(2.87)
- интеграл в граници от -2.87
до +2.87.
Използвайте, че F'(Х) = 2F(Х)
- 1.
Вижте решението
на задачата.
Задача 6. Задача 6. За
нормално
разпределение с m =
3.44 и s
=
0.39 намерете от приложение
1 F(4.56),
където F(4.56)
е интеграл в граници от -![]() до 4.56.
до 4.56.
Вижте решението
на задачата.
Задача 7. За нормално разпределение с m = 3.44 и s = 0.39 намерете от приложение 1 интеграл в граници от 2.32 до 4.56. Използвайте, че F'(Х) = 2F(Х) - 1. Вижте решението на задачата.
Автор: Пламен Пенчев, Ph.D.
[ това е материал от брой 24 от октомври 2008 г. на списание "Коснос" www.kosnos.com ]