С този материал започнахме една поредица за приложение на статистиката в химията. Материалът може да се използва не само от химици, а от всички, които се занимават с обработка на експериментални резултати. В тази лекция ще разгледаме някои статистически разпределения.

Задача 1. Вероятността случайната величина да заема стойности в интервала  (-, +)  е единица. Докажете това за нормалното разпределение - съответният интеграл няма решение, но двойният интеграл по-долу може да се реши със замяна на променливите x и y с радиални координати r и q.

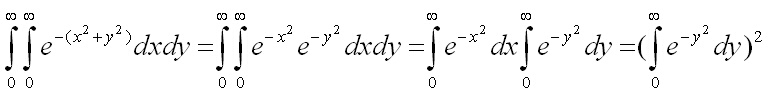
Решение:

Вкарваме m, корен от 2 и s² в диференциала dx, а след това понеже подинтегралната функция е симетрична функция, разделяме този интеграл на две области, които обединяваме (понее са равни). При което получаваме значително по-просто изглеждащ интеграл.

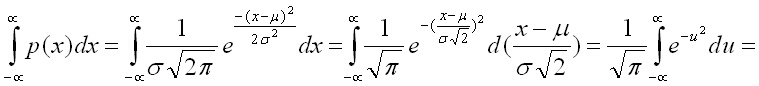
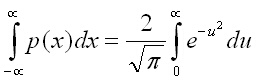
Този интеграл е нерешим в явен вид, но е равен на корен квадратен от следния двоен интеграл:

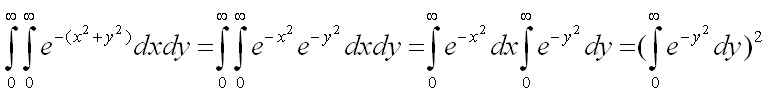
Но двойният интеграл може да се реши чрез смяна на променливите x = rcos(q) и y = rsin(q), при което се получава

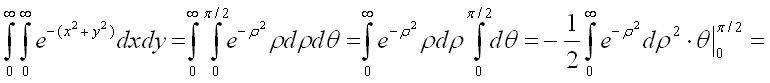
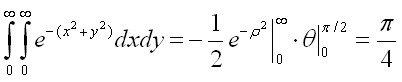
Т.е първоначалният интеграл е равен на:

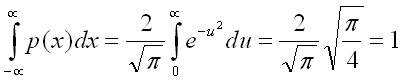
Задача 2. Намерете математическото очакване и дисперсията на равномерното разпределение.

Решение:

Разбиваме цялата област на интегриране на три интервала, в които плътността на вероятността на нормалното разпределение има различни значения - нула извън интервала (a, b) и константа в този интервал.

За математическото очакване се получава:

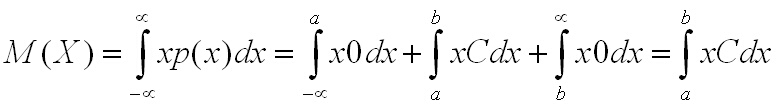
Взимаме предвид, че в интервала (a, b) плътността е C = (b - a)/2 (вижте този материал) и получаваме.

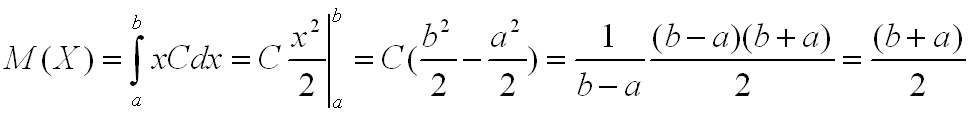
За дисперсията се получава:

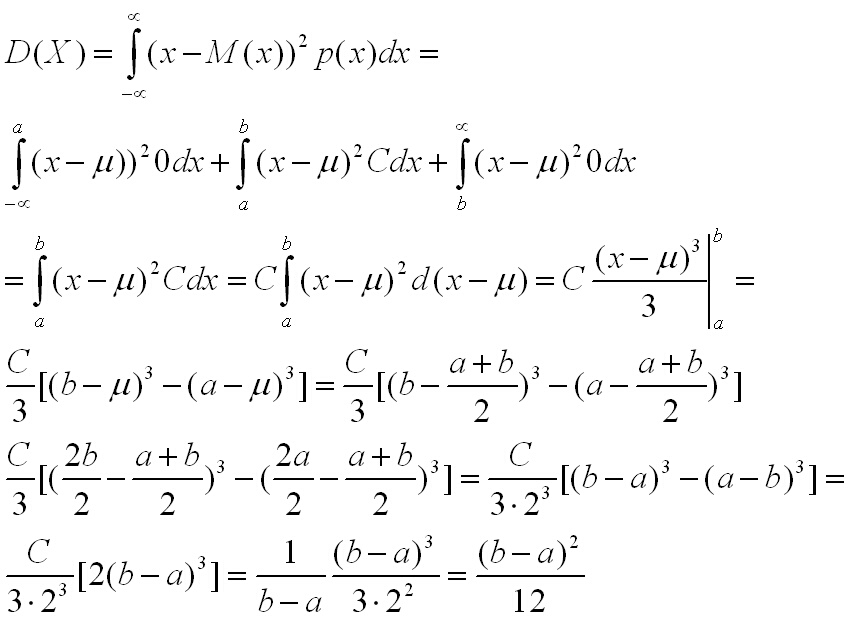
Задача 3. Докажете, че математическото очакване и дисперсията на нормалното разпределение са съответно m и s².

Решение: И при двата интеграла сменяме променливата x с y = (x - m)/s, при което се получава x = (sy + m) и dx = sdy, както и интегралните граници остават същите = ( - m)/s  и - = (- - m)/s.

За математическото очакване се получава:

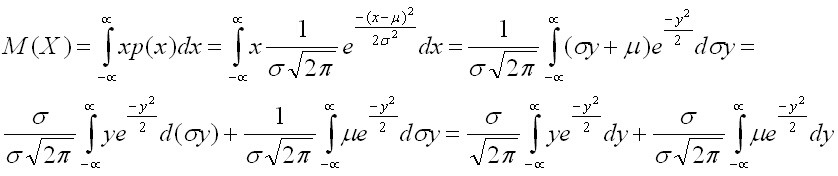
Първият интеграл е интеграл от нечетна функция в симетрични граници и затова е равен на нула, а последсният интеграл беше решен в Задача 1 (по-горе) и е равен на корен от пи.

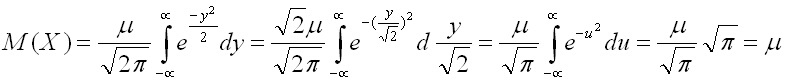
Вместо да решаваме последния интеграл може да го запишем в позната форма

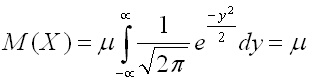
За дисперсията се получава:

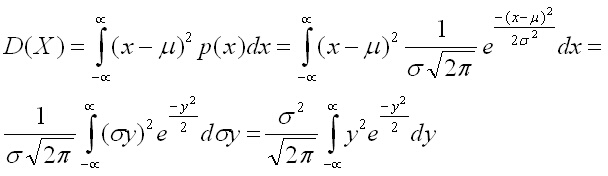
Този интеграл може да го интегрираме по части, за целта вкарваме експоненциалната функция под диференциала

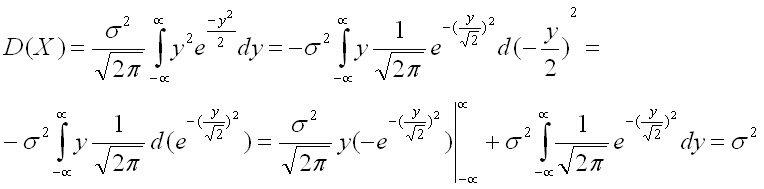
Първият интеграл е нула, а последният интеграл е интеграл от плътността на вероятността на стандартното разпределение (т.е. нормално разпределение с m = 1 и s² = 0) и е равен на единица.

Задача 4. За стандартното разпределение докажете, че F'(Х) = 2F(Х) - 1, където F(Х) е интеграл в граници от - до X, а F'(Х) - интеграл в граници от -X до +X. Използвате симетричността на Гаусовата крива.

Решение:

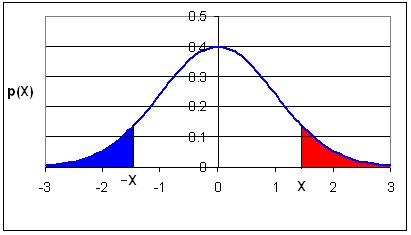
По-горе е дадена плътността на вероятността на стандартното разпределение. Интегралът F(Х)е равен на площта под кривата от - до червено-оцветената площ, а площта под цялата крива е единица. Стандартното разпределение е симетрично относно нулата и затова червената площ е равна на синята площ на графиката. Червената площ е 1 - F(Х), т.е. и синята площ е същата. Тогава F'(Х) ще е площта под кривата между двете оцветени площи и тя ще е равна на F(Х) - (1 - F(Х)) или 2F(Х) - 1.

Задача 5. За стандартното разпределение намерете от приложение 1  F'(2.87) и F(2.87), където F(2.87) е интеграл в граници от - до 2.87, а F'(2.87) - интеграл в граници от -2.87 до +2.87.  Използвайте, че F'(Х)=2F(Х)-1.

Решение:

От приложение 1 намираме, че F(2.87) = 0.99795. Следователно F'(2.87) = 2xF(2.87) - 1 = 2x0.99795 - 1 = 0.9959.

Задача 6. За нормално разпределение с m = 3.44 и s = 0.39 намерете от приложение 1  F(4.56), където F(4.56) е интеграл в граници от - до 4.56.

Решение:

Подобно на задача 3 сменяме променливата x с y  = (x - m)/s, при което се получава x = (sy + m) и dx = sdy, както и интегралните граници стават 2.87 = (4.56 - m)/s = (4.56 - 3.44)/0.39  и -= (- - m)/s.

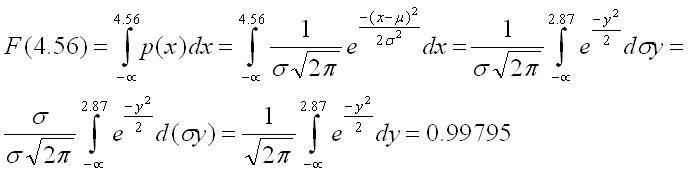
Последният интеграл е интеграл от плътността на стандартното разпределение и него го взехме от приложение 1.

Видяхме, че с помощта на таблицата на функцията на разпределение на стандартното разпределение, дадена в приложение 1, можем да намерим функцията на разпределение на нормално разпределение с произволни математическо очакване и дисперсия: за целта нормираме интегралната граница по формулата y  = (x - m)/s.

Задача 7. За нормално разпределение с m = 3.44 и s = 0.39 намерете от приложение 1 интеграл в граници от 2.32 до 4.56.  Използвайте, че F'(Х) = 2F(Х) - 1.

Решение:

Сменяме интегралните граници по формулата y  = (x - m)/s, при което се получават следните нови интегрални граници  (т.е. тези за стандартното разпределение) 2.87 = (4.56 - m)/s = (4.56 - 3.44)/0.39  и -2.87 = (2.32 - 3.44)/0.39. Това е интеграл от плътността на стандартното разпределение в симетрични граници и може да бъде намерен по формулата F'(2.87) = 2xF(2.87) - 1 = 2x0.99795 - 1 = 0.9959.(сравнете със задача 5)

Автор: Пламен Пенчев, Ph.D.