В предишния материал се запознахме с физичните основи на ЯМР спектроскопията и въведохме някои зависимости между основните ядрени величини. Така написани тези зависимости се изпълняват за ядра без електронна обвивка. Електронната обвивка на атомите в молекулата променя магнитното поле около ядрата и по този начин влияе на резонансната им честота. И тъй като тази обвивка е свързана със строежа на молекулите, то ЯМР играе изключително важна роля в химията.

1. Екраниране на магнитното поле от електроните. Локалното магнитно поле около ядрото на протия в молекулата B_loc е различно от приложеното магнитно поле B₀. Относителната промяна на това поле се отбелезва със s и се нарича константа на екраниране (shielding constant):

Константа на екраниране има много малка величина - от порядъка на милионни части. Според квантово-механичната теория тя може да се представи като сума от три константи, които представляват трите основни фактора, от които тя зависи:

Първата константа отразява диамагнитното (diamagnetic) екраниране на електроните около ядрото, втория - парамагнитното (paramagnetic) екраниране на електроните около ядрото, а третата константа отчита екранирането от всички съседни групи.

2. Химично отместване. Уравнение (1) от предишния материал добива следния вид:

Вижда се, че резонансната честота зависи от константата на екраниране, която от своя страна зависи от електронната плътност около ядрото на протия, а последната от своя страна зависи от електронния строеж на молекулата като цяло. Както казахме, тази зависимост прави ЯМР важен за химията. Но резонансната честота зависи и от силата на магнитното поле B₀ и това води до необходимост при представянето на ¹H-ЯМР спектри (подобно на фигура 1 от предишния материал) да се рапортува и силата на магнитното поле. Допълнително константата на екраниране е много малка - от порядъка на милионни части - и изследователите ще трябва да боравят с величини на n с точност до 7-я знак: например да сравняват два сигнала от типа на 59.60457 MHz и 59.60451 MHz за апарат с B₀ = 1.4T. Ето защо ¹H-ЯМР спектрите се представят по специален начин: на абсцисата стои разликата между константата на екраниране на определени протони на вещество, избрано за стандарт, и константата на екраниране на протоните в изследваното съединение. Тази разлика се нарича химично отместване (chemical shift) и се означава с d.

Тъй като константата на екраниране е безразмерна величина, то и химичното отместване е безразмерно, но поради малката му стойност то се изразява в милионни части (ppm, part per million) и на практика формула (3) е:

което е едно и също, защото ppm = 10^-6.

Стандартното вещество се нарича още референтно вещество (reference), а избраните негови протони - референтни протони. В българския език се употребяват още изразите еталонно вещество и еталон.

На практика се измерват резонансните честоти на референтните протони n_r и протоните на изследваното съединение n_x: ето защо химичното отместване се представя като следното отношение:

Ако се замести уравнение (2) в (4) след съкращаване на фактора (g/2p)B₀ се получава уравнение (3)

В горните уравнения (1 - s_x) беше заменено с 1, тъй като s_x е от порядъка на милионни части и е много по-малко от единица.

Самата замяна на (1 - s_x) с единица води до израза по-долу

който може да се тълкува като

където n₀ е честотата на апарата. И трите уравнения (3) или (3а), (4) и (5)  означават едно и също нещо, стига да са избрани едни и същи референтни протони на едно и също референтно вещество.

3. Стандартни вещества в ЯМР. Най-разпространеният стандарт в протонния ЯМР е тетраметилсиланът, TMS, Si(CH₃)₄. Неговите 12 протона са химически и магнитно еквивалентни и дават остър интензивен сигнал - т.е. може да се използват малки количества от TMS. Тези протони са силно екранирани, което води до s_r > s_x , т.е. d > 0 за повечето вещества X. Освен това TMS е относително инертно вещество и не реагира с повечето от органичните съединения, и затова може да бъде добавяно непосредствено в епруветката с проба, откъдето лесно се отстранява при нагряване, защото TMS е много летлив.

Като еталонни вещества се използват също и циклохексан, хлороформ и бензен. Тогава химичното отместване може лесно да се преизчисли спрямо TMS. Ако d(R)_X е химичното отместване на веществото X спрямо друго еталонно съединение R, а d(TMS)_X е химичното отместване на веществото X спрямо TMS, то имаме

откъдето следва, че

В горния израз заменихме s_TMS - s_R с d(TMS)_R. Получихме че химичното отместване на протоните на изследваното съединение X спрямо TMS е равно на химичното отместване на протоните на изследваното съединение X спрямо друго референтно съединение R събрано с химичното отместване на референтното съединение спрямо TMS.

Така написани, формулите важат за използването на референтното съединение като вътрешен стандарт, т.е. то е добавено непосредствено в епруветката с проба. Има специални епруветки, в които има тънка капиляра, в която се добавя чисто референтното съединение без то да се смесва с пробата, която се изследва. Измереното химично отместване в този случай ще е различно и за целта има формули [1,2,3], по които то се преизчислява към това, получено с използване на вътрешен стандарт.

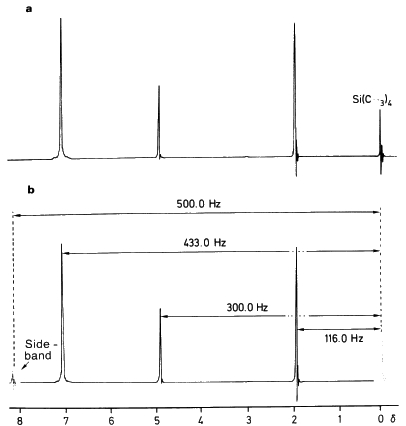
На фигура 1 е даден ¹H-ЯМР спектър на бензил ацетата, CH₃COOCH₂C₆H₅. Резонансната честота на апарата е 60 MHz. Ивицата на петте фенилови протона излиза на разстояние 433.0 Hz от ивицата на TMS, т.е. n_x - n_r = 433.0 Hz и по формула (5) химичното отместване на тези протони ще е

Съответно, химичното отместване на метиленовите протони в горния спектър ще бъде

а химичното отместване на метиловите протони ще бъде

От дадения пример ясно се вижда, че химичното отместване нараства отдясно наляво (както и резонансната честота), което е обратно на традицията за представяне на стойностите по абсцисата. Ето защо преди години бе направен неуспешен опит да се въведе друга скала, наречена "тау скала", която да замени широкоизползваната "делта скала", която бе разгледана по-горе. Стойностите по двете скали са свързани с уравнението

Очевидно, за горните три сигнала химичните отмествания по тау скалата ще са съответно t(ph) = 2.78 ppm , t(CH₂) = 5.00 ppm и t(CH₃) = 8.07 ppm.

Видяхме, че сигналите могат да се представят по три начина: в честотни разлики като n_x - n_TMS, в делта скалата и в тау скалата. За първото представяне е необходимо да се даде и честотата на апарата, за да може да се сравнява спектъра със спектри, заснети на апарати с други работни честоти.

4. Спин-спиново взаимодействие. По-горе споменахме, че константа на екраниране може да се представи като сума от три константи:

В третата част на сумата, s_neighb, освен известните електронни ефекти - индукционен и мезомерен - се включва и влиянието на ядрата на съседните протони. Както беше отбелязано в първата лекция, ядрото на протия има магнитен момент. Този ядрен магнитен момент взаимодейства с магнитния момент на електроните, които обкръжават ядрото. Те променят своето движение (ориентация на магнитния момент) и тази промяна може да се предаде на съседните електрони и те от своя страна да променят обкръжението на съседно ядро. Т.е. ориентацията на ядрения магнитен момент на съседните протони променя екранирането на протона, който е в резонанс.

Нека разгледаме спектъра на 1,1,2-трихлоретана, даден на фигура 2.

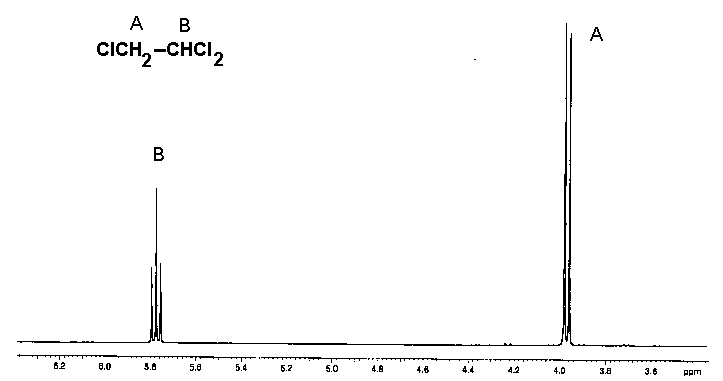
Фигура 2. 300 MHz ¹H-ЯМР спектър на 1,1,2-трихлоретан.

Сигналът на метиленовите протони, означени като A, е двукратно разцепен (дуплет), а този на метиновите протони, означени като B, - трикратно разцепен (триплет) - вижте фигура 2.

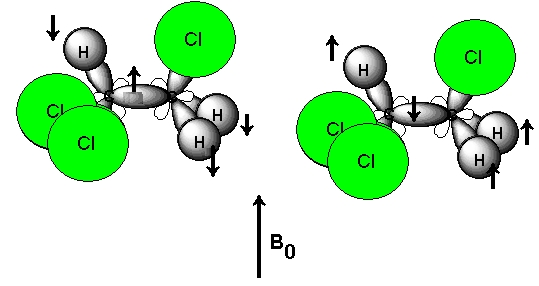
Причината за двукратното разцепване на сигнала на метиленовите протони A е, че когато те са в резонанс, магнитният момент на метиновият протон B може да има две ориентации - паралелно на полето и антипаралелно на полето - вижте фигура 3. Съответно този момент се предава на електроните на сигма връзката C-H_B, чрез нея на електроните на sp³ хибридната орбитала C-C и накрая на електроните на сигма връзката C-H_A. Тъй като нивата на ядрата на H_B протоните са почти еднакво заселени (разликата е 0.001%, вижте задача 2 от предишния материал), то в половината молекули ефективното магнитно поле край A протоните ще се усилва, а в другата половина ще отслабва. Т.е. при половината молекули протоните A ще встъпват в резонанс при по-висока честота (лявата ивица на сигнала A), а в другата половина при по-ниска честота (дясната ивица на сигнала A). Това може да се изобрази така:

Когато H_B протоните са резонанс H_A протоните на метиленовата група могат да бъдат ориентирани по четири различни начина:

Комбинацията в ляво има сумарен магнитен момент -1/2 + -1/2 = -1, средните две състояния имат сумарен магнитен момент 1/2 + -1/2 = 0, а тази в дясно - сумарен магнитен момент 1/2 + 1/2 = 1. Т.е. при 1/4 от молекулите локалното поле ще се намалява, при 2/4 от молекулите то няма да се променя и при 1/4 то ще се усилва. Затова сигналът ще е разцепен на три с отношение на интензитетите 1/4 : 2/4 : 1/4, което в цели числа е 1 : 2 : 1.

Аналогично в съединението 1,1-дихлоретан, Cl₂CH-CH₃, сигналът на метиновият протон ще е разцепен четири пъти в отношение 1 : 3 : 3 : 1, защото възможните ориентации на магнитния момент на ядрото на съседните протони метилови протони ще е:

Тези съотношения на интензитетите в съответния мултиплет могат да се изчислят по триъгълника на Паскал, в който числата във всеки следващ ред се получават като се сумират две от горностоящите числа:

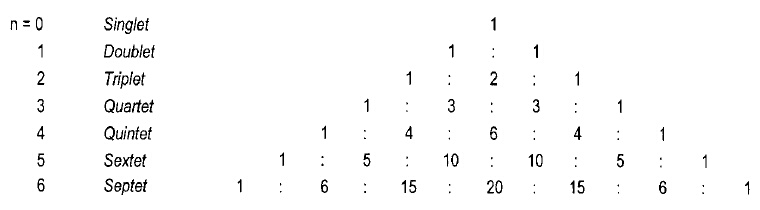
Например, при наличие на пет съседни протона сигналът ще е секстет с отношение на интензитетите в него така както 1:5:10:10:5:1 .

В разгледаните по-горе случаи на спин-спиново взаимодействие се предполагат две неща: (1) разстоянието между сигналите на взаимодействащите протони е значително по-голямо от разцепването на сигналите, и (2) всички съседни протони си взаимодействат по един и същи начин с протона в резонанс. Спектрите, за които важи първата предпоставка се наричат в литературата "спектри от първи порядък" (first order spectra). В следващия материал ще разгледаме по-подробно спин-спиново взаимодействие.

1. Harald Gunter. NMR-Spektroscopie: Grundlagen, Konzepte und Anwendung der Protonen und Kohlenstoff-13 Kernresonanz-Spektroscopie in der Chemie. Georg Thieme Verlag, Stuttgart, 1992.

2. Ст. Спасов, М. Арнаудов. Приложение на спектроскопията в органичната химия, Изд. "Наука и изкуство", София, 1978.

3. Ст. Спасов, Л. Каменов. Ядрен магнитен резонанс в органичната химия, Изд. "Наука и изкуство", София, 1973.

4. Eberhard Breitmaier. Structure Elucidation By NMR In Organic Chemistry: A Practical Guide. John Wiley & Sons, Ltd., 2002.

5. Joseph B. Lambert, Eugene P. Mazola. NMR_Spectroscopy. Pearson Eduaction Inc., 2001.

Кредити: фигури 1 и 2 са взети от книгата на Гюнтер [1], а схемата за триъгълника на Паскал от книгата на Брайтмайер [4].

Автор: Пламен Пенчев, Ph.D.