(Set Theory)
С този материал започваме една поредица по отделни теми в математиката, които са полезни за образованието на химици, физици, инженери и други, които се занимават с прилагане на математиката в различните науки и производства. Съдържанието и структурата на всяка една лекция ще следва плътно тези на съответния материал в превъзходната книга на Том Апостол [1].
В математиката под множество се разбира сбирка на обекти от произволно естество, като отделният обект се разглеждат като едно цяло без да става въпрос за някаква негова структура. Примери за такава сбирка са племе, стадо, тълпа, отбор, колекция, електорат. Отделните обекти в множеството се наричат елементи на множеството и се казва, че те принадлежат на множеството или че то е съставено от тях или че то ги притежава.
Математиците се интересуват главно от множества от математически обекти, като множества от числа, множества от криви, множества от геометрични фигури и даже множества от други множества. Ако няма никаква информация за типа на елементите на множеството то това множество се нарича абстрактно множество.
1. Означаване на множества. Те се означават предимно с главни латински букви - A,B,C,X,Y,Z а техните елементи с малки латински букви - a,b,c,x,y,z. Фактът че елементът x принадлежи на множеството S се означава по следния начин:
x О S
Ако елементът x не принадлежи на множеството това се означава с задраскан вертикално символ П по следния начин:
x П S
Понякога е удобно някои множества да бъдат отбелязвани, чрез изброяване на елементите им, затворени в големи скоби. Това означение се нарича списъчно означение на множества (roster notation). Например, {2,3,5,9} или {2,4,6, ...}, където последното множество е безкрайно изброимо и е множеството на всички положителни четни цели числа: многоточието означава един вид изброяване на останалите елементи.
Аналогично можем да записваме множествата и по следния начин
A = {x| f(x)}
където с x е означен кой да е елемент на множеството, а f(x) е някакво условие, което изпълняват всички елементи на множеството. Това означение се нарича списъчно означение на множества (roster notation).
Например множесвото на всички цели положителни четни числа се записва по този начин:
A = {n| n=2k, к е цяло положително число}
Всъщност в горния пример условието се състои от две твърдения, съединени с логическия оператор и (and).
За да е пълна и непротиворечива теорията на множествата се разглежда и множеството, което няма нито един елемент - така нареченото празно множество (empty set). То се означава със следния символ Ж и по следния начин Ж = {}.
2. Равенство на множества. Първата концепция (идея) е равенството на две множества, което се дава със следната дефиниция:
Дефиниция 1: Две множества са равни едно на друго, ако се състоят от едни и същи елементи. Това се записва по този начин: A = B. Ако едното множество притежава поне един елемент, който не е елемент на другото множество тогава те не са равни и това се означава по следния начин: A =/= B. (знакът е равно със задраскана вертикална наклонена черта, но ние сме го изписали по този начин, понеже няма такъв знак в кодовите таблици)
Подредбата на елементите в множеството, както и тяхното повторение нямат никакво значение, затова според горната дефиниция долните три множества са равни:
{2,3,5,9} = {3,2,9,5} = {2,2,3,5,5,9}
3. Подмножество на дадено множество. За дадено множество A можем да създадем няколко други множества, за които се казва че са негови подмножества. Например множеството на целите положителни числа по-малки от десет и делими на 4, {2,8}, е подмножество на множеството на целите положителни четни числа по-малки от десет {2,4,6,8}.
Дефиниция 2: Множеството B e подмножество (subset) на множеството A, ако всеки елемент на B е елемент и на A. Казва се, че B се съдържа в A, или че A съдържа B. и това се означава с една от двете релации (отношения) Н и К по следния начин BНA или AКB. Двете релации се наричат включване на едно множество в друго.Също така се казва, че A е надмножество (superset) на B.
За да е пълна и непротиворечива теорията на множествата празното множество е подмножество на всички множества, т.е. ЖНA или {}НA .
Твърдението BНA въобще не изключва твърдението AНB и ако и второто отношение е изпълнено то лесно се доказва, че двете множества са равни, т.е. имаме
BНA Щ AНB ЬЮ A = B
където символът Щ означава логическия оператор и (and), а символът ЬЮ - необходимо и достатъчно условие от едното да следва другото, т.е. ако е изпълнена лявата част, то следва дясната и ако е изпълнена дясната, то следва лявата.
Ако имаме BНAЩ A=/=B то се казва, че B е несобствено подмножество (aproper subset) на A и това се означава по един от следните два начина BМA и AЙB.
Обикновено в приложенията на теорията на множествата имаме едно множество, което се явява надмножество на всички разглеждани в приложението множества. То се нарича универсално множество (universal set) и обикновено другите множества се записват чрез някакво условие, което задоволяват елементите на множествата. Нека, например, универсалното множество е множеството на всички натурални числа N (целите положителни числа) то тогава всички записани по-долу множества са негови подможества:
{n| n=2k Щ кОN} - множеството на всички четни натурални числа;
{n| n=2k-1 Щ кОN} - множеството на всички нечетни натурални числа;
{l| l<7 Щl>2 Щ lОN} = {3,4,5,6};
{n| Щ (к<2Ък>10)} - множеството на всички натурални числа по-големи от десет или равни на единица (символът Ъ означава логическото или, or).
Когато универсалното множество (в горните примери N) се подразбира ще записваме тези множества без кОN, например първото като {n| n=2k}.
Трябва да се отбележи, че елементът x се различава от множеството, което съдържа само този елемент {x}. Това изискване е необходимо за да има непротиворечивост на теорията на множествата. По същия начин, Ж и {Ж} са две различни множества, които не са равни: Ж=/={Ж}.
4. Обединение и сечение на множества. За всеки две множества A и B може да се образува трето множество C, наречено обединение (union), елементите на което са елементи на A или на B. Разбира се, даден елемен на C може да е едновременно елемент на A и B, но това се подразбира от логическия оператор или. Обединението се означава по следния начин:
C = AИB
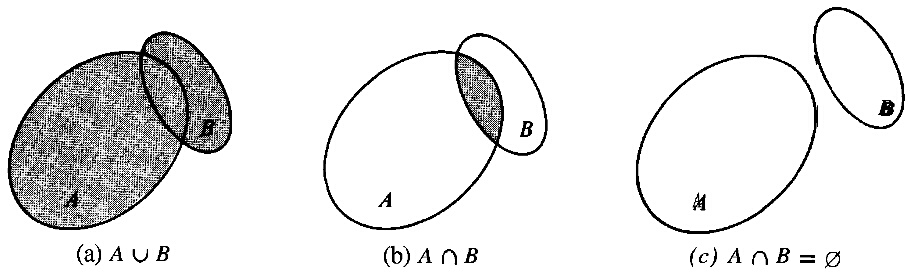
Точките в една равнина (например тази на листа хартия или тази на компютърния екран) образуват едно универсално множество от точките в тази равнина, и отделните подмножества на това универсално множество са участъци от листа хартия (петна), които се представят с точките в тях. Това не само са множества от точките в една равнина, но и са добър модел за визуализация множествата, който може да се използва за проверка на повечето логически твърдения, свързани с множествата. Такива диаграма като тези на фигура 1 се наричат диаграми на Вен (Venn diagrams).
Лявата диаграма на фигурата дава нагледно обединението на множествата - това е защрихованата площ, средната - тяхното сечение, като сечението също е представено със защрихованата площ, а дясната показва, че двете множества имат нулево сечение - т.е. тяхното сечение е нулевото множество.

Сечение на две множества A и B се дефинира като множество, чийто елементи са елементи едновременно на A и B. Сечението се отбелязва с оператора З по следния начин C = AЗB. Когато AЗB=Ж казваме, че двете множества A и B са несвързани (disjoint).
Например, ако A = {1,2,3} и B = {3,4,5}, тогава AИB = {1,2,3,4,5} и AЗB = {3}.
5. Разлика на множества. Разликата на две множества, C = A-B, се нарича множество, което съдържа само тези елементи на A, които не са елементи на B. На фигура 1 незащрихованата площ на A е разликата A-B, а незащрихованата площ на B - разликата B-A. Разликата A-B още се нарича допълнение на B относително A.
Например, ако A = {1,2,3} и B = {3,4,5}, тогава A-B = {1,2} и B-A = {4,5}.
Трите операции между множества имат големи прилики с операциите събиране, умножение и изваждане на числа, но също така имат и съществени разлики. Например двете операции обединение и сечение са комутативни и асоциативни, подобно на събирането и изваждането, а разликата не е нито комутативна, нито асоциативна, подобно на разликата при числата.
AИB = BИA и AЗB = BЗA (1)
AИ(BИC) = (AИB)ИC и (AЗB)ЗC = AЗ(BЗC) (2)
A-B =/= B-A
(A-B)-C =/= A-(B-C)
За верността на последното неравенство може да се убедим със следния пример A = {1,2,3}, B = {3,4} и C = {3,2,5},тогава
(A-B)-C = ({1,2,3} - {3,4}) - {3,2,5} =
{1,2} - {3,2,5} = {1}
и
A-(B-C) = {1,2,3} - ({3,4}) - {3,2,5}) =
{1,2,3} - {4} = {1,2,3}
За обединението и сечението важи и дистрибутивния закон
AЗ(BИC) = (AЗB)И(AЗC) и AИ(BЗC) = (AИB)З(AИC) (3)
Забележете, че първото равенство по-горе прилича на дистрибутивния закон при числата - a(b+c) = ab + ac, докато второто прилича на a+(bc) = (a+b)(a+c), което не е вярно!
Всички тези свойства от (1) до (3) може да се докажат строго логически като се използва дефиницията на операциите.
Ще въведем следните означения, които са подобни на тези за сума и произведение на числа
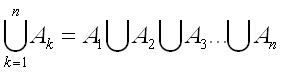 и
и 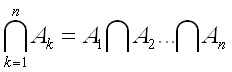
В заключение ще запишем няколко свойства на операциите между множества, чието доказателство оставяме на читателя като задача.
AИB = BИA и AЗB = BЗA (1)
AИ(BИC) = (AИB)ИC и (AЗB)ЗC = AЗ(BЗC) (2)
AЗ(BИC) = (AЗB)И(AЗC) и AИ(BЗC) = (AИB)З(AИC) (3)
AИA = A и AЗA = A (4)
AНAИB и AЗBНA (5)
AИЖ = A и AЗЖ = Ж (6)
Задачи
Задача 1. Нека R е множеството на всички реални числа. Запишете следните множества в т.н. списъчно означение. Вижте решението на първия пример.
a) A = {x| x2-1 = 0 Щ xОR} = {-1,1}
b) B = {x| x2-2x+1 = 0 Щ xОR} c)C = {x| x3-2x2+x = 0 Щ xОR}
d) D = {x| x2-13x+42 = 0 Щ xОR} e)E = {x| x2+10 = 9 Щ xОR}
Вижте отговорите
на задачата.
Задача 2. Нека A = {1,2} и B = {1}. Кои от релациите (отношенията) са верни?
a) AМB b) AНB c) BОA d) AЗB = {1}
e) AИB=A f) AИB=B g) 1ОB h) 1МA i) {1}МA
j) BМA k) BНA
Вижте отговорите на задачата.
( виж другите учебни материали )
Литература
[1] Tom M. Apostol; Calculus, vol. 1, John Wiley, 1967.
Автор: Проф. Процесор Аритметиков
[ това е материал от брой 27 от февруари 2009 г на списание "Коснос" www.kosnos.com ]
Отговори на задачите
b) B = {x| x2-2x+1 = 0 Щ xОR} = {1}
c)C = {x| x3-x2+x = 0 Щ xОR} = {0}
d) D = {x| x2-13x+42 = 0 Щ xОR} = {6,7}
e)E = {x| x2+10 = 9 Щ xОR} = {} = Жограмиран
Отговори на задача 2. A = {1,2} и B = {1}.
a) AМB - не вярно b) AНB - не вярно:
Пояснение за двата отговора: A има един елемент, 2, който B няма.
c) BОA - не вярно: множеството B не е елемент на А.
d) AЗB = {1} - вярно е.
e) AИB=A - вярно е.
f) AИB=B - не е вярно.
g) 1ОB - вярно е.
h) 1МA - 1 е елемент на А (и на B), но не множество, затова не е вярно твърдението.
i) {1}МA - вярно е.
j) BМA - вярно е.
k) BНA - вярно е. грае , полиморфизъм switch if else ?
[ това е материал от брой 27 от февруари 2009 г на списание "Коснос" www.kosnos.com ]