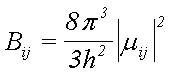 (1)
(1)
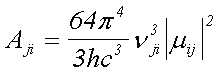 (2)
(2)
1. Вероятност за преход, подборни правила. При феноменологичните разглеждания на процесите на поглъщане и излъчване, Айнщайн въвежда представите за вероятностите за преход между енергетичните нива, като разглежда три механизма:
1. Преходи от по-ниски на по-високи нива, свързани с поглъщане на енергетичен квант от лъчението, т.н. възбуждане.
2. Преходи от по-високи на по-нискоенергетични нива, под действие на външно възбуждащо лъчение, т.н. индуцирано излъчване (на основата на тази хипотеза по-късно бяха създадени източниците на кохерентно лъчение).
3. Самопроизволни преходи от по-високи на по-нискоенергетични нива.
Вероятността за спонтанни (самопроизволни) преходи Аi,j, и вероятността за абсорбционни (принудени) преходи Bi,j, се дават съответно с изразите:
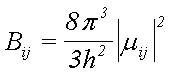 (1)
(1)
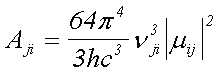 (2)
(2)
Следователно вероятността за извършване на един оптичен преход е пропорционална на квадрата на матричния елемент на диполния момент на прехода mi,j между началното състояние i и крайното състояние j, описвани с вълновите функций Yi и Yj, съответно:
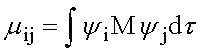 (3)
(3)
където mi,j e матричният елемент на диполния момент, характеризиращ прехода iаj, а M е операторът на собствения електричен диполен момент на молекулата.
За система, притежаваща n енергетични нива, матричните елементи на диполния момент mi,j се записват във вида:

Диагоналните елементи на матрицата mi,j представляват диполните моменти на молекулата в съответните стационарни състояния, а извъндиагоналните mi,j - диполните моменти на прехода от едно стационарно състояние в друго.
От (1) и (2) следва, че вероятността за преход зависи и при двата процеса от квадрата на матричния елемент на диполния момент mi,j, който от своя страна се описва съответно с вълновите функции Yi и Yj.
Ако вълновите функции Yi и Yj са известни може да се пресметне дали тези две състояния могат да се комбинират помежду си, т.е. да се получат подборните правила за прехода. Например при едноелектронни системи mi,j е нула (изчезва) при всички случаи, освен когато квантовото число I = +1 ( правило на подбор). Когато mi,j = 0, разглеждания преход е забранен като диполен преход. Ако mi,j e различен от нула преходът се класифицира като разрешен.
Ако вълновите функции на двете състояния не са известни, заключения за подборните правила могат да се правят въз основа на техните симетрични свойства. Когато Yi и Yj имат еднаква симетрия преходите са забранени; разрешени са преходи само между състояния с различна симетрия.
От изложеното следва, че преходи между две енергетични състояния ще се извършват при различни условия за различните движения. Наличието на собствен електричен диполен момент е задължително условие за извършване на въртеливи преходи, т.е. за наблюдаване на ротационни спектри на въртящи се молекули. Вибрационен спектър на абсорбция или емисия ще може да се наблюдава само в случай, че диполният момент на молекулата се променя при трептене на атомите. За разлика от спектрите на ротация и вибрация, при електронни спектри, предварителното условие за наличие на диполен момент в изследваната молекула не е наложително. Тъй като всеки електронен преход е по принцип свързан с ново преразпределение на електроните това води до промяна или възникване на диполен момент в молекулата.
Освен с момента на прехода интензитетът на абсорбционните ивици се характеризира още с т.н. сила на осцилатора f. Силата на осцилатора се определя от отношението на действителния интензитет и интензитета на излъчване на електрона, разглеждан като тримерен хармоничен осцилатор. За такъв "идеален електрон" f = 1. Чрез силата на осцилатора преходите се класифицират, като се свързва теорията с експеримента. За разрешен преход f=1; за единична симетрична ивица
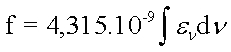 (4)
(4)
където интегралът по-горе е площта под кривата.
За практническо пресмятане на силата на осцилатора се използува израза:
f = 4.6.10-9emaxDn1/2, (5)
където emax e моларната абсорбируемост, а Dn1/2 - полуширина на ивицата. (За смисъла на интеграла в (4) вижте материала "Закон за абсорбция на светлината")
2. Населеност на енергетичните нива. В повечето от досегашните разглеждания се считаше в неявен вид, че се разглежда взаимодействието на една единствена микрочастица с един фотон. На практика обаче се работи с множество идентични частици, които имат определена енергия при определени условия. Броят частици N, които се намират в определено стационарно състояние, т.е. които са населили дадено енергетично ниво, се определя от две величини: абсолютната температура Т и енергетичната разлика DЕ между двете нива, напр. Еi и Еj: (DЕ = Еi - Еj).
Съгласно закона на Болцман, за система, намираща се в термодинамично равновесие, отношението на броя частици между двете нива Еi и Еj: се дава с израза:
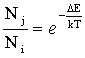 (6)
(6)
където k е константата на Болцман; k = 1.381.10-23 [J K-1].
При определена температура, населеността на дадено енергетично ниво Еj зависи само от енергетичната разлика DЕ. Когато тази разлика DЕ >> kT, по-нискоенергетичното ниво е много по-силно населено от възбуденото, т.е. Ni >> Nj. Колкото двете нива са по-близко разположени едно до друго (Еi@Еj), толкова отношението Nj/Ni клонr към 1, с други думи, разликата между броя на молекулите в двете нива е много малка (Ni@Nj).
Отношението на броя молекули в основно към броя молекули в първо възбудено електронно енергетично състояние, например за l = 800 [nm], при стайна температура (300 К), се дава съгласно (6):
Първо намираме енергетичната разлика, която е
DЕ = Е1 - Е0 = hc/l =
= 6.63x10-34 [J s] *.3x108 [m.s-1] / 8x10-7 [m] =
= 2.49x10-19 [J]
После използваме отношението (6):
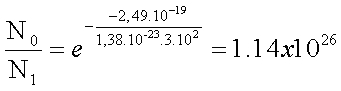
(В горния израз нулевото ниво е с по-ниска енергия и DЕ < 0, затова има два знака минус в експонента, което на практика прави аргумента му положителен и отношението по-голямо от единица, което показва, че повече частици са в нулевото ниво, отколкото в първо възбудено.)
Отношението на населеностите Nj/Ni зависи също от температурата на системата; при промяна на температурата се променя и Nj/Ni, особено в случаите, когато разликата между енергиите на нивата е малка в сравнение с топлинната енергия. Например, отношението на населеностите Nj/Ni при`n = 4000 cm-1 e следното:
при 300 К Nj/Ni
= 2.2x108
при 400 К Nj/Ni
= 1.8x106
От изложеното следва, че при термодинамично равновесие и възбуждане по топлинен път най-силно заселено ще бъде основното състояние. При повишаване на температурата ще се населват все по-високостоящи енергетични нива.
В някои случаи е възможно едно по-високо енергетично ниво да бъде заселено по-силно от основното. Този процес, наречен инверсно заселване, намира приложение при създаване на лазерни лъчения.
3. Ширина и форма на спектралните линии и ивици. От разглежданията в лекцията "Взаимодействие между електромагнитното лъчение и веществото" следва, че поради наличие на фина структура, вибрационните и електронни спектри са съставени от ивици с определена ширина. Една друга, чисто техническа причина за регистириране на спектрални ивици, а не на линии, е крайната ширина на процепите на дисперсионните спектрометри. Независимо от качествата на монохроматора, в приемника попада не монохроматично лъчение, а сноп с значителна полихроматичност, поради което спектрометърът регистрира не безкрайно тесен сигнал (теоретичния), а ивица с определена ширина. (Това е т.н. конволюиран сигнал; коволюцията е явление, което се наблюдава при всяко апаратурно измерване и е причина за загуба на информация). Подобряването на качествата на спектрометъра може да доведе до известно повишаване на неговата разделителна способност, но не неограничено. На всеки енергетичен преход, атомен или молекулен, съответствува една минимална, гранична ширина, наречена естествена ширина на линиите или ивиците. Естествената ширина на спектралните линии е обратно пропорционална на времето на живот и не може да бъде намалена чрез никакви способи.
Наред с описаните причини от апаратурен характер съществено влияние за уширяване на спектралните линии имат също така Доплеровият ефект, сблъскванията на частиците и принципа за неопределеност на Хайзенберг.
1. Доплерово разширение. При движение на поглъщащи или излъчващи частици към наблюдателя, дължината на вълната на лъчението се отмества късовълново (синьо), т.е. честотата расте. Обратно - излъчването на частици, които се движат с голяма скорост от наблюдателя е отместено дълговълново (червено отместване). При наличие на голям брой частици в термодинамично равновесие се осъществяват и двата процеса, в резултат на което спектралните ивици се разширяват.
2. Сблъскване на частиците. Поради непрекъснатото движение, атомите и молекулите на газовете и течностите често се удрят помежду си и със стените на съда, което е причина за моментното им деформиране, а следователно и до известно смущаване на енергетичните им състояния - електронни, вибрационни и ротационни. В резултат на това някои допълнителни преходи стават разрешени, а съответните им ивици - активни.
Спектрите на твърдите тела, поради ограничена възможност за движение на молекулите в тях, притежават тесни ивици. Причина за това биха могли да бъдат също разцепвания на ивиците поради влияние на кристалното поле.
3. Принцип на неопределеност на Хайзенберг. Енергетичните нива дори на изолирани атоми и молекули не могат да бъдат безкрайно тесни, поради действието на принципа на Хайзенберг за неопределеност на енергията и времето. Според последния, ширината на едно спектрално ниво DЕ [J] и средното време на живот Dt [s] са свързани в зависимостта:
DЕ Dt @ h/2p @ 10-34 [J s], (7)
където h е константата на Планк.
От (7) следва, че колкото е по-широко дадено енергетично ниво, толкова времето на живот е по-кратко. Обратно, времето на живот ще бъде безкрайно дълго за безкрайно тесни нива, какъвто е случаят с основните енергетични нива на микрочастиците. Наистина, давайки на DЕ стойност нула, за времето на живот Dt се получава безкрайност от което следва, че системата може да остане в най-ниското енергетично състояние неограничено дълго време.
Времето на живот в дадено възбудено електронно състояние е около 10-8s, тогава за стойността на енергията получаваме:
DЕ @ h/(2pDt) @ 10-34/10-8 = 10-26 J
Един преход между това състояние и основното ще има неопределеност на енергията DЕ и свързана с нея неопределеност на честота
Dn = DЕ/h @ 1/(2pDt)
Dn@ 1/(2p10-8) = 108 Hz
Следователно, за едно енергетично състояние с време на живот 10-8s неопределеността на честотата108 Hz. Тази неопределеност в случая е малка в сравнение с естествената ширина на електронния преход (1010 - 1014 Hz) и не оказва съществено влияние върху ширината на ивиците.
При възбудени спинови електронни състояния обаче които съществуват около 10-7s, неопределеността в честотата е 107 Hz. Тъй като честота на такива преходи (обикновено 108 - 109 Hz) е съизмерима с уширението, неопределеността на Хайзенберг има много голям ефект върху ширината на ивиците.
Особено значение от експериментална гледна точка има т.н. полуширина на спектралните ивици Dn1/2. Под полуширина се разбира ширината на ивицата при половината от интензитета, когато последният се измерва в абсорбционни единици. Ако един спектър е получен в единици пропускливост Т, стойностите трябва да се преизчислят в абсорбция. Това се налага много често при определяне на Dn1/2 в инфрачервената спектроскопия.
Естествената форма на спектралните ивици се представя с някои математически изрази, най-често с функциите на Гаус и Лоренц. Реалните спектрални ивици могат да се представят приближено (да се апроксимират) чрез линейна комбинация от Гаусова и Лоренцова функции, като участието на всяка от тях е различно в различните случаи. Например Доплеровото разширение се описва от функцията на Гаус, а взаимодействието между частиците - от функцията на Лоренц. Когато спектралните ивици се представят като функция на вълновото число те са почти симетричини; при представянето на ивиците като функция на дължината на вълната те са несиметрични и са отместени към по-големите дължини на вълната.
При опитно измерваните спектри, формата на ивиците се усложнява допълнително от тяхното припокриване и поради наличието на фон на спектъра. Под фон се разбира една непрекъснато променяща се с честотата абсорбция, върху която са наложени абсорбционните ивици на веществото.
Литература
1. Г. Андреев. Молекулна спектроскопия, Изд. ПУ “П. Хилендарски”, Пловдив, 1999.
Автор: проф. дхн Георги Андреев