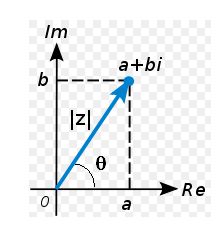
Фигура 1.
Графично представяне на комплексно число.
Числата, които са пропорционални на i се наричат комплексни числа. Например 2.314xi е едно такова число (с x сме отбелязали знака за умножение). Видяхме, че аритметичните операции, които са дефинирани за реалните числа, нямат резултат само реални числа и резултатът от тях излиза извън областта на реалните числа: имагинерно = операция(реално). По същия начин, прилагането на аритметичните операции върху имагинерни числа води до реални, например i2 = -1. И за да няма противоречии се въвеждат т.н. комплексни числа, които представляват сума от реално и имагинерно число: z = a + ib.
1. Комплексни числа. Те са сума от две числа - реално и имагинерно число, z = a+ ib. Числото a се нарича реална част на z, а числото b - имагинерна част на z, като те се отбелязват съкратено с x = Re(z) и y = Im(z). Обикновено, комплексните числа се представят като наредена двойка от две реални числа: z = (a, b). Аритметичните операции с тях се дефинират непротиворечиво, ако се приеме, че действаме с един вид полиноминален израз и спазваме дефиницията i2 = -1.
Две комплексни числа, (a1, b1) и (a2, b2), се събират или изваждат като се събират или изваждат съответните им части:
(a1, b1) + (a2, b2) = (a1+a2, b1+b2)
(a1, b1) - (a2, b2) = (a1-a2, b1-b2)
Всяко комплексно число z има спрегнато число на него, което се отбелязва с чертичка над него `z или със звезда след него z*. То има същата реална част, но неговата имагинерна част е обратна по знак:
z =
(a, b)
`z
= (a, -b)
Както споменахме, вместо като наредени двойки, комплексните числа могат да се записват и като сума, в която имагинерната част се преставя във вид на произведение на имагинерното число i (корен от минус единица) и имагинерната част. Например (a, b)= a + ib. Този запис позволява по-лесно извършване на аритметичните действия с комплексните числа: например за събирането получаваме:
(a1,
b1) + (a2,
b2) =
= (a1
+
ib1) + (a2 + ib2) =
= a1
+
a2 + ib1 + ib2 =
= (a1
+
a2) + i(b1 + b2) =
= (a1+a2,
b1+b2)
По същия начин може да се получи и произведението на две комплексни числа, само трябва да се има предвид че i2 = -1 .
(a1,
b1) x (a2, b2) =
= (a1
+
ib1) x (a2 + ib2)
=
= a1a2
+
i2b1b2 + ia1b2 +
ia2b1 =
= a1a2
-
b1b2 + i(a1b2 + a2b1)
=
= (a1a2
-
b1b2, a1b2 + a2b1)
където с x сме отбелязали знака за умножение.
От тази формула се вижда, че произведението на едно комплексно число по неговото спрегнато дава реално число, което е равно на сума от квадратите на частите на комплексното число.
z`z
= (a, b) x (a, -b) =
= (aa + bb,
ab - ab)
= (a2
+ b2, 0)
Корен квадратен от това произведение се нарича модул на комплексното число и се бележи с |z| или Mod(z). Тази величина още се нарича големина на комплексното число или негова абсолютна стойност.
Като използваме горната формула и като умножим числителя и знаменателя с комплексно спрегнатото на делителя, за частното на две комплексни числа получаваме:
z1
/ z2 =
= (a1,
b1) / (a2,
b2) =
= z1`z2
/ z2`z2
=
= [(a1
+
ib1)(a2 - ib2)] / [(a2 + ib2)(a2
-
ib2)] =
= (a1a2
-
i2b1b2 - ia1b2 +
ia2b1) / (a22 +
b22) =
= (a1a2
+
b1b2 + i(a2b1 - a1b2))
/ (a22 + b22) =
= [(a1a2
+
b1b2)/(a22 + b22),
(a2b1 - a1b2)/(a22+
b22)]
Останалите действия с комплексните числа, както и тяхното експоненциално представяне (формула на Ойлер) ще бъдат разгледани в специална лекция в списанието ни.
2. Формула на Ойлер. Комплексното число може да се представи и в експоненциална форма по следния начин:
z = |z|еiq
където |z| е абсолютната стойност (модул) на z, а q - неговият аргумент (наричан още фаза). Връзката между абсолютната стойност и аргумента, от една страна, и реалната част и имагинерната част, от друга, се дават със следните формули (Sqrt е корен квадратен, а atan е аркустангенс):
|z| = Sqrt(a2 + b2)
q = atan(b/a)
a = |z|cos(q)
b = |z|sin(q)
Комплексното число може да се представи и като точка в равнината, в която е дефинирана правоъгълна координатна система. Реалната координата на числото a представлява абсцисата на точката, а имагинерната b - нейната ордината - вижте фигура 1. Ако се прекара вектор от началото до точката на комплексното число (синята стрелка на фигура 1), то неговата дължина съответства на модула на комплексното число |z|, а ъгълът между този вектор и абсцисата представлява неговия аргумент q.

Фигура 1.
Графично представяне на комплексно число.
На фигура 2 е представено комплексното число z = 3 + 4i. Неговият модул по горните формули е
|z| = Sqrt(32 + 42) = Sqrt(25) = 5
q
= atan(4/3) = 0.9273 rad = 53.13 deg
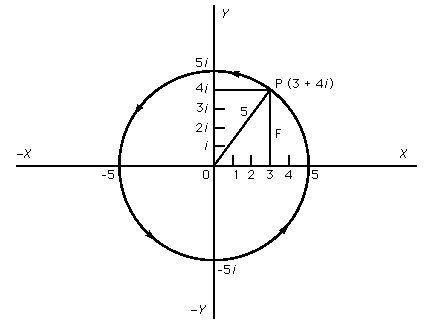
Фигура 2.
Графично представяне на комплексното число 3
+ 4i.
3. Корен n-ти от комплексно число. За всяко едно комплексно число z има n на брой комплексни числа wk; k = 0, 1, ... n-1, които удовлетворяват равенството wkn = z. Т.е. всяко едно комплексно число има n на брой n-ти корени. Ако комплексното число z се представи в експоненциална форма z = |z|еiq, където |z| е абсолютната стойност на z, а q - неговият аргумент, то k-ият n-ти корен се намира по следния начин wk = |w|еi(q + k2p)/n, където реалното число |w| е n-ти корен от реалното число |z|, т.е. |w|n = |z|.
Нека намерим 4-те квадратични корена на реалното число -16, т.е. комплексното число (-16, 0). Модулът на това число е 16 и реалният квадратичен корен от него е 2, защото 24 = 16. Неговата фаза е 180 deg или в радиани 3.1415926 rad (p rad). Тогава неговите четири корени ще са:
|z|k = |w|еi(q + k2p)/n = 2еi(p + k2p)/4; k = 0, 1, 2, 3
или
|z|0 = |w|еi(p + 0x2p)/4 = 2еip/4
|z|1 = |w|еi(p + 1x2p)/4 = 2еi3p/4
|z|2 = |w|еi(p + 2x2p)/4 = 2еi5p/4
|z|3 = |w|еi(p + 3x2p)/4 = 2еi7p/4
В горните формули с x сме означили операцията умножение.
На фигура 3 са представени 4-те квадратични корена на реалното число -16, т.е. комплексното число (-16, 0).
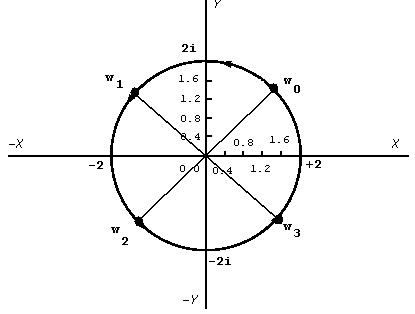
Фигура 3.
Графично представяне на 4-те квадратични корена на реалното число -16.
.
( вижте
другите учебни материали )
.
Литература
.