Симетрия на молекулите
част втора

Операции на симетрия - обобщение

В предишната лекция се запознахме с операциите на симетрия и елементите на симетрия, които съответстват на тези операции. Разбрахме се, че обект на операциите на симетрия ще бъдат химичните молекули, които се разглеждат като набор от ядрата на атомите и химичните връзки между атомите, които се изобразяват чрез отсечки между тях - това е така наречения sticks and balls model. Напълно възможно е, а от друга страна - доста плодотворно, разглеждане на молекулата като набор от съответните молекулни орбитали (МО), които са линейни комбинации от атомни орбитали (ЛКАО): тогава прилагането на операциите на симетрия дава много полезни резултати за вида и свойствата на тези МО. В тази лекция засега ще бъде използвано единствено първото представяне на молекулите.

Операцията на симетрия е действие, което не променя вида на молекулата, и което действие е тясно свързано със съответния елемент на симетрия. Реално в химията операциите на симетрия играят по-съществена роля от елементите на симетрия. Това е така, защото всичките операциите на симетрия съставляват една група в алгебрата - т.е. те са обект на изучаване на алгебрата, за който обект има стройна и последователна математическа теория.

Нека разгледаме молекулата на борния хидрид, BH₃. Това е планарна (равнинна) молекула, в която атомът на бора е разположен по средата, а трите атома на водорода са по върховете на един равностранен триъгълник.

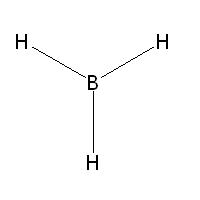
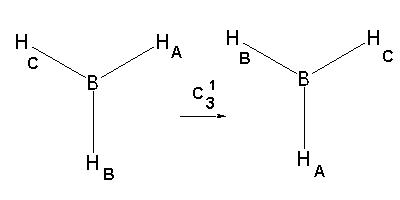
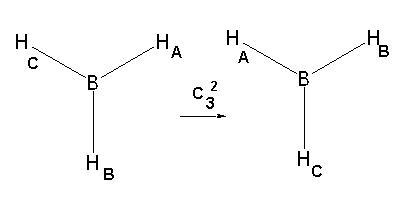
Тази молекула има една ос на симетрия C₃, която е разположена перпендикулярно на равнината на молекулата и минава през борния атом. С тази ос на симетрия, обаче, са свързани две операции на симетрия - първата, означена като C₃¹, е завъртане на молекулата на 120^o по часовниковата стрелка, и втората, означена като C₃²,  - завъртане на молекулата на 240^o по часовниковата стрелка.
 

В този случай - на ос от трети порядък - втората операция на симетрия може да се разглежда като завъртане на 120^o, но в посока, обратна на часовниковата стрелка. По-правилно е операциите от този вид да се означават като завъртане на даден ъгъл в една посока - в общия случай при ос от порядък n, C_n, имаме n операции на симетрия и за n > 3 е удобно използването на една и съща посока на завъртане. Тези операции се означават като C_n¹, C_n², ... C_n^n-1,  и C_nⁿ (всъщност последна операция съвпада с операцията на идентичност: C_nⁿ = E) и представляват завъртане на молекулата на ъгли 360/n, 360*2/n ... 360*(n-1)/n и 360*n/n.

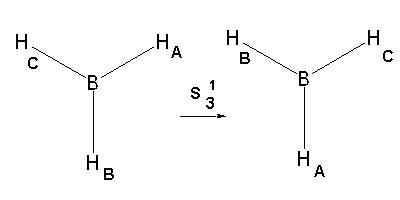
Молекула на BH₃ има и две операции на несобствено завъртане, които съответстват на ос от трети порядък S₃. Съответно те се означават с S₃¹ и S₃². Подобно на операцията на собствено завъртане C₃³, което съвпада с Е, несобственото завъртане S₃³ съвпада с операцията s_h.
 

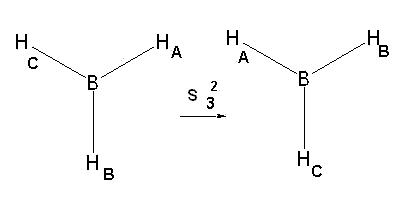На практика резултатите от тяхното извършване съвпадат с горните две операции на собствено завъртане, но това е следствие от това, че равнината, в която се отразяват атомите на молекулата след завъртането, съвпада с молекулната равнина (молекулата лежи в нея). В следващата лекция е даден пример на молекула, със същата симетрия и нележаща в една равнина.

Молекула на BH₃ има и три операции на симетрия C₂, чиито оси от втори порядък лежат в молекулната равнина и минават през борния атом и през един от водородните атоми. Молекулата има и три вертикални равнини на симетрия, s_v, които са перпендикулярни на молекулната равнина, s_h. Т.е. има три операции на отражение през вертикална равнина на симетрия и една операция на отражение през хоризонтална равнина на симетрия. По-долу са дадени всичките 12 на брой операции на симетрия, които притежава молекулата.

Е, 2C₃, 3C₂, s_h , 2S₃, 3s_v

Така написани тези 12 операции са групирани в 6 класа на операции на симетрия, като в първи клас има една операция (Е), във втори - две (двете собствени завъртания C₃), в трети три и т.н. Винаги броят на операциите на симетрия в даден клас дели общия брой операции на симетрия. С цел различаване на трите операции C₂ ще ги отбелязваме с буквата на атома, през който минава оста на симетрия C₂, т.е. C₂(A) означава, че молекулата е завъртяна през ос, която минава през атом A. По същия начин ще различаваме и трите операции s_v, след които в скоби ще поставяме означението на атома, през който минава вертикалната равнина s_v.

Тези операции на симетрия както казахме в предишната лекция образуват група в алгебрата. Групата в алгебрата е съставена от елементи за които е дефинирана операцията "умножение" (т.е. комбиниране на два елемента), която операция е асоциативна и резултатът от това "умножение" * (комбиниране) е винаги елемент, който принадлежи на групата. Т.е. ако означим елементите на групата с a, b, c и d то имаме

(a * b) * c  = a *( b * c) = d, и  е d принадлежи на групата

Има още две други изисквания: (1) в групата да има елемент на групата, наречен "единичен елемент", който умножен с кой да е елемен да дава последния:

e * b = b     и   b * e  = b

и (2) всеки елемент на групата да има обратен елемент, за който

b^-1 * b = e     и   b * b^-1  = e

където e е единичния елемент. Операцията "умножение" не е задължително да бъде комутативна, т.е. в общия случай не се изпълнява a * b  = b * a.

Практически, с лист хартия и молив, читателят може да провери дали тези условия се изпълняват за 12 операции на симетрия на групата на симетрия, която описва молекулата на борния хидрид. (Тази група се означава с D_3h, но в следващата лекция ще се дискутират групите на точкова симетрия на молекулите).

Правилото за умножение на операции на симетрия е последователното им изпълнение. Например, C₃¹ * s_v(A) е еквивалентно на следното - завъртане на 120^o и последващо отражение в една от вертикалните равнини (нека изберем тази, която минава през атома H_A).

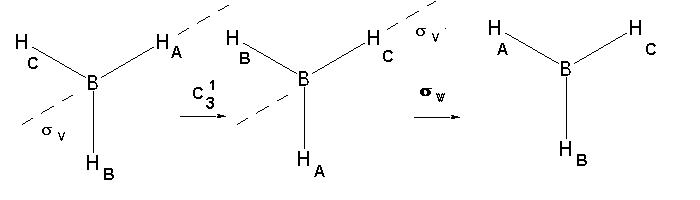
Реално, тази промяна на водородните атоми е евквивалентна на отражение през вертикалната равнина на симетрия, която минава през атом B.

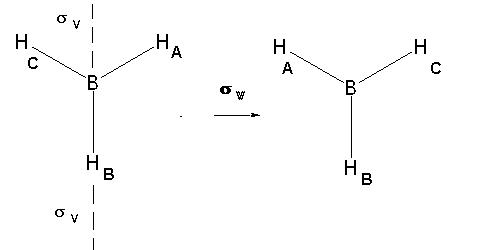
Т.е. s_v(A) * C₃¹ = s_v(B), където в скоби е указан водородният атом, през който минава вертикалната равнина на симетрия. За умножението на тези операции на симетрия важи следната таблица (първа се извършва операцията в първия ред, а след нея операцията в първата колона, а в таблицата стои резултатната операция):
 

Op1 * Op2

Е

C31

C32

C2(A)

C2(B)

C2(C)

sh

S31

S32

sv(A)

sv(B)

sv(C)

Е

Е

C31

C32

C2(A)

C2(B)

C2(C)

sh

S31

S32

sv(A)

sv(B)

sv(C)

C31

C31

C32

Е

C2(C)

C2(A)

C2(B)

S31

S32

sh

sv(C)

sv(A)

sv(B)

C32

C32

Е

C31

sv(B)

sv(C)

sv(A)

S32

sh

S31

sv(B)

sv(C)

sv(A)

C2(A)

C2(A)

C2(B)

sv(C)

Е

C31

C32

sv(A)

sv(A)

sv(C)

sh

S31

S32

C2(B)

C2(B)

C2(C)

sv(A)

C32

Е

C31

sv(A)

sv(C)

sv(A)

S32

sh

S31

C2(C)

C2(C)

C2(A)

sv(B)

C31

C32

Е

sv(C)

sv(A)

sv(C)

S31

S32

sh

sh

sh

S31

S32

sv(A)

sv(B)

sv(C)

Е

C31

C32

C2(A)

C2(B)

C2(C)

S31

S31

S32

sh

sv(C)

sv(A)

sv(B)

C31

C32

Е

C2(C)

C2(A)

C2(B))

S32

S32

sh

S31

sv(B)

sv(C)

sv(A)

C32

Е

C31

C2(B)

C2(C)

C2(A)

sv(A)

sv(A)

sv(B)

sv(C)

sh

S31

S32

C2(A)

C2(B)

C2(C)

Е

C31

C32

sv(B)

sv(B)

sv(C)

sv(A)

S32

sh

S31

C2(B)

C2(C)

C2(A)

C32

Е

C31

sv(C)

sv(C)

sv(A)

sv(B)

S31

S32

sh

C2(C)

C2(A)

C2(B)

C31

C32

Е

Лесно може да се провери, че всяка една операция на симетрия има обратна - комбинирането им не води до промяна на номерирането на атомите в молекулата. Например за отражението през хоризонталната равнина на симетрия, s_h, самата тази операция е обратна на себе си, т.е. s_h * s_h = E. Същото е с отраженията във вертикалните равнини на симетрия, s_v - второто такова отражение дава идентична молекула, т.е. s_v(A) * s_v(A) = E. На операцията C₃¹ обратна е C₃², а на S₃¹ обратна е S₃². Очевидно, същото е изпълнено за вторите операции - първите са техните обратни операции.

В тази лекция разгледахме по-подробно операциите на симетрия и видяхме, че на един елемент на симетрия може да съответства повече от една операция на симетрия. Също така въведохме комбинирането на операциите на симетрия - така нареченото умножение в групата на симетрия. Видяхме, че произведението на две операции на симетрия дава друга операция на симетрия, която е от същата група на симетрия, и че всички операции на симетрия имат свои обратни операции. В следващата лекция ще се запознаем с точковите групи на симетрия и ще научим как да определяме химичните молекули каква група на симетрия имат, в зависимост от техните операции на симетрия.

Автор: Пламен Пенчев, Ph.D.
Авторски права: Материалът или част от него могат да се използват свободно (копирани на друг сайт) в обучението на български или македонски студенти само ако в сайта изрично се цитира тази оригинална статия във вида: П.Пенчев, Симетрия на молекулите. Част 2., Списание "Коснос" (www.kosnos.com), брой 3, 2007 г.