Симетрия на молекулите
част трета

Умножение на операциите на симетрия

В предишните две лекции [лекция 1] и [лекция 2] се запознахме с операциите на симетрия и елементите на симетрия, които съответстват на тези операции. Във втората лекция обобщихме понятието операция на симетрия като показахме, че на един елемент на симетрия може да съответстват няколко операции на симетрия. Също така въведохме умножението на операциите на симетрия, и показахме на каква операция на симетрия е равнозначно последователното изпълнение на две операции на симетрия. В лекцията представихме следната таблица, от която може да се изведе резултата на умножението на няколко операции на симетрия. Предмет на настоящата лекция е един от начините за извеждане на тази таблица - с помощта на произведения на матрици.

Таблица 1. Умножение на операциите на симетрия (от лекция 2). Първа върху молекулата се извършва операцията Op2, дадена в първия ред, а след нея операцията Op1, дадена в първата колона, а в таблицата стои резултатната операция Op1 * Op2.
 
Op1 * Op2
Е
C31
C32
C2(A)
C2(B)
C2(C)
sh
S31
S32
sv(A)
sv(A)
sv(C)
Е
Е
C31
C32
C2(A)
C2(B)
C2(C)
sh
S31
S32
sv(A)
sv(B)
sv(C)
C31
C31
C32
Е
C2(C)
C2(A)
C2(B)
S31
S32
sh
sv(C)
sv(A)
sv(B)
C32
C32
Е
C31
sv(B)
sv(C)
sv(A)
S32
sh
S31
sv(B)
sv(C)
sv(A)
C2(A)
C2(A)
C2(B)
sv(C)
Е
C31
C32
sv(A)
sv(A)
sv(C)
sh
S31
S32
C2(B)
C2(B)
C2(C)
sv(A)
C32
Е
C31
sv(A)
sv(C)
sv(A)
S32
sh
S31
C2(C)
C2(C)
C2(A)
sv(B)
C31
C32
Е
sv(C)
sv(A)
sv(C)
S31
S32
sh
sh
sh
S31
S32
sv(A)
sv(B)
sv(C)
Е
C31
C32
C2(A)
C2(B)
C2(C)
S31
S31
S32
sh
sv(C)
sv(A)
sv(B)
C31
C32
Е
C2(C)
C2(A)
C2(B))
S32
S32
sh
S31
sv(B)
sv(C)
sv(A)
C32
Е
C31
C2(B)
C2(C)
C2(A)
sv(A)
sv(A)
sv(B)
sv(C)
sh
S31
S32
C2(A)
C2(B)
C2(C)
Е
C31
C32
sv(B)
sv(B)
sv(C)
sv(A)
S32
sh
S31
C2(B)
C2(C)
C2(A)
C32
Е
C31
sv(C)
sv(C)
sv(A)
sv(B)
S31
S32
sh
C2(C)
C2(A)
C2(B)
C31
C32
Е

В таблицата означенията са същите като в предната лекция, където те съответстват на молекулата на BH3: например sv(A) е вертикална равнина на симетрия, която минава през оста C3и връзката BHA. Тук сме запазили тези означения, въпреки че работим с различна молекула, която е със същата симетрия (D3h), т.е. има същите елементи и операции на симетрия. В тази лекция под C2(A) ще разбира ос от втори порядък, която минава през центъра на триъгълната призма, перпендикулярна е на ръба AF и е успоредна на медианата (която е и височина и ъглополовяща) от върха А в триъгълника ABC. Аналогично се дефинират останалите две оси C2. Под sv(A) ще разбираме вертикална равнина на симетрия, която минава през осите C3 и C2(A).

Трябва да отбележим, че тук работим с неравнинна молекула, поради необходимостта от преобразования на атомите в други атоми при операциите на симетрия sh, S31 и S32: в равнинната молекула на BH3 тези операции ще действат като операцията на идентичност E, т.е. нямат да променят номерацията на водородните атоми.

1. Матрица на дадена номерация на атомите в симетрична молекула.
Нека разгледаме следната молекула, която е съставена от 6 еднакви атома A, B, C, D, E и F, които лежат по върховете на една правилна триъгълна призма.

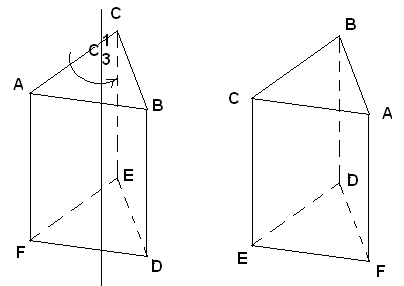
Фигура 1. Преобразуване на молекулата при операция на симетрия C31.

На фигурата е представена не само молекулата, но и резултатът от операцията C31, която премества атом А на мястото на атом B, B - на мястото на C, и т.н. Ако номерираме тези атоми с числата от едно до шест, то тази номерация на атомите може да се представи с една матрица, която се състои от 6 реда и 6 колони, където всяка една нейна колона (вектор-стълб) съответства на даден атом. На следната фигура са показани тези вектор-стълбове, а на следващата фигура - матрицата, която е съставена от тях.

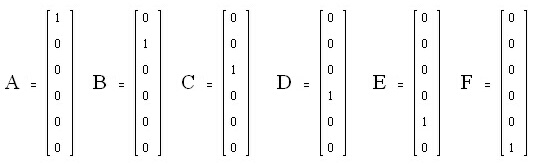
Фигура 2. Вектор-стълбовете, които съответстват на атомите A, B, C, D, E и F.

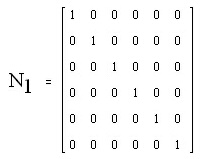
Фигура 3. Матрицата, която е съставена от вектор-стълбовете на A, B, C, D, E и F.

Смисълът на единиците в матрицата е следният - например, първа колона в матрицата (или първи вектор-стълб от фигура 2) отговарят за атом A, а положението на единицата от първа колона в първи ред означава оригиналната номерация на атом А. Ако атом А премине в друг атом при някоя операция на симетрия, то единицата от първата колона преминава в ред, чийто номер съответства на номера на колоната, съпоставена на другия атом. Или казано за вектор-стълбовете, вектор-стълбът на атом А преминава във вектор-стълба на друг атом.

2. Матрица на дадена операция на симетрия в симетрична молекула.
Засега въведохме матриците (или вектор-стълбовете), които съответстват на дадена номерация на атомите в симетричната молекула. От друга страна, на операцията на симетрия съответства една матрица 6 на 6, която умножена по вектор-стълба, дава вектор-стълба на другия атом, чието място заема преобразувания атом. На следваща фигура е представена матрицата, която съответства на операцията на симетрия C31, както и умножението на тази матрица с вектора-стълб, който съответства на атома A.

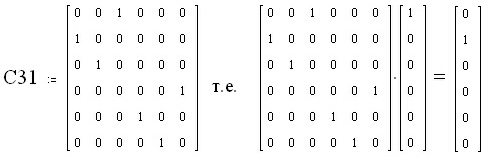
Фигура 4. Матрицата на операцията на симетрия C31 и нейното умножение с вектор-стълба на атом A.

Ако се прегледат едновременно фигури 2 и 4 се вижда, че в резултат на умножението се получава вектор-стълбът на атом B. По същия начин умножението на матрицата C31 води до трансформации на другите атоми, еднакви с трансформациите на операцията на симетрия C31. Ако се умножат двете матрици C31 (от фигура 4) и N1 (от фигура 3) ще се получи новата номерация на атомите, т.е. както споменахме атом А се премества на мястото на B, B - на мястото на C, и т.н.

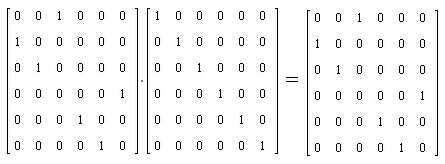
Фигура 5. Умножение на матрицата на операцията на симетрия C31 с матрицата на оригиналната номерация на атомите от фигура 1 (матрицата на номерацията е на фигура 3).

Тъй като матрицата на първоначалната номерация N1 е единична, то самата матрица C31 на операцията на симетрия съответства на новата номерация на атомите! В получената матрица от фигура 5 (а и в матрицата C31) единиците са на позиции (2,1), (3,2), (1,3) и т.н., което означава, например за първата позиция, че при операцията на симетрия C31 атомът с номер 1 (т.е. атом A) е преминал на мястото на атома с номер 2 (т.е. атом B). Ако се сравнят фигури 1 и 5 ясно се вижда съответствието между геометричната смяна на местата на атомите, от една страна, и първата и третата матрици от фигура 5, от друга страна.

И за останалите операции на симетрия могат да се съставят матрици, които им съответстват. Просто самата матрица на операцията на симетрия ще съответства на новата номерация, която се получава при разместване на атомите. Например, операцията на симетрия sv(C) преобразува по следния начин атомите в разглеждана молекула със симетрия на правилна триъгълна призма:

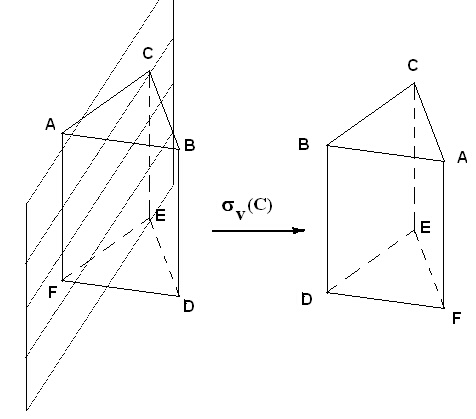
Фигура 6. Преобразуване на атомите при операцията на симетрия sv(C). Атоми A и B си сменят местата, както и D и F. Равнината sv(C) минава през атоми C и E и средата на отсечката AB.

Съответната матрица на тази операция е дадена на фигура 7, където е показано и преминаването на атом A в атом B чрез умножението на метриците svC и N1.

Фигура 7. Матрицата на операцията на симетрия sv(C).

Аналогично на разсъжденията, направени по фигура 5, и тук забелязваме, че единиците в матрицата svC са на позиции (2,1), (1,2), (3,3) и т.н., което означава, например за първата позиция, че при операцията на симетрия sv(C) атомът с номер 1 (т.е. атом A) е преминал на мястото на атома с номер 2 (т.е. атом B). Но в матрицата svC има и единици, които стоят на диагонала. Ето защо вече можем да обобщим значението на положението на единиците в матриците на симетрия по следния начин: (1) единиците, които стоят на диагонала показват, че съответния атом (с номер, равен на номера на реда) не се променя при операцията на симетрия, и (2) едниците, които стоят в колона k и на ред l показват, че при операцията на симетрия атом k преминава в атом l. Това обобщение ни позволява лесно да съставяме на матриците на операциите на симетрия!

3. Умножение на матриците на операциите на симетрия в симетрична молекула.
Ако умножим двете матрици C31 и svC се получава нова матрица - това умножение е представено на фигура 8.

Фигура 8. Умножението на двете матрици  дава матрица, която съответства на операцията на симетрия svB.

Получената матрица съответства на размяна на атоми A и C - единиците, които стоят в позиции (3,1) и (1,3), както и на размяна на атоми E и F - това са единиците, които стоят в позиции (5,6) и (6,5). На диагонала има две единици - едната е на ред 2, а другата на ред 4. Това показва, че атоми с номера 2 и 4, т.е. атоми B и D не променят местата си при операцията на симетрия, която е резултат от извършването последователно на операциите sv(C) и C31. Очевидно това е операцията sv(B), която разменя тези двойки атоми - и точно този резултат е даден в таблица 1.
 
С помощта на умножение на такива матрици могат да бъдат съставени таблиците на умножение на всички точкови групи на симетрия. Могат да се използват редица програми, които поддържат работата с матрици, например MathCAD или Excel. Във файла symmetry.xls са дадени матриците на останалите операции на симетрия, както и някои действия с тях. Не трябва да се забравя, че ако матриците са умножени в реда A*B, то върху молекулата първо се извършва операцията на симетрия B, а после операцията A. Любознателният читател може да провери таблица 1 с помощта дадения Excel файл.

Автор: Пламен Пенчев, Ph.D.
Авторски права: Материалът или част от него могат да се използват свободно (копирани на друг сайт) в обучението на български или македонски студенти само ако в сайта изрично се цитира тази оригинална статия във вида: П.Пенчев, Симетрия на молекулите. Част 3., Списание "Коснос" (www.kosnos.com) брой 4, 2007 г.