С този материал започнахме една поредица за приложение на хемометриката в химията. В тази лекция ще разгледаме моделирането на химичния експеримент.

Резултатът на един химичен експеримент зависи от много фактори, както случайни, така и неслучайни. Всички те не могат да бъдат отчетени посредством теоретични съображения, ето защо необходим етап от провеждането на експеримента е неговото планиране и оптимизиране. Оптимизирането на експеримента е процес, с помощта на който се намират оптималните условия (оптималните стойности на неслучайните фактори) за неговото провеждане. Когато е необходима задълбочена информация за химичния експеримент, се извършва неговото моделиране, т.е. отразяване на неговите свойства върху друг обект. Като един от най-разпространените модели се е наложил математичният модел на експеримента, позволяващ с най-малко средства да се постигнат поставените цели - изучаване, моделиране, оптимизиране и прилагане на химичния експеримент.

1. Моделиране. Моделът е обект, чийто съставни части съответстват на тези на първообраза и между тях са налице връзки, аналогични на връзките в първообраза. Обикновено в модела са застъпени не всички съставни части и връзки в моделирания обект; избират се само онези, които по мнението на експериментатора са най-важни и значими. Например може да се изработи електричен модел на химичната реакция A + B а C, при който на количествата на A, B и C може да се съпоставят величините напрежения на електрическия ток, които да се изменят подобно на променящите се количества на веществата A, B и C. Но също така може да се направи математичен модел на тази реакция, който да представлява уравнение, даващо зависимостта на величината С от други две величини А и В във всеки един момент от времето. За разлика от електричния модел, математичният е евтин, с неограничено време на живот и лесно преобразуваем, при откриване на допълнителна зависимост (например влиянието на температурата).

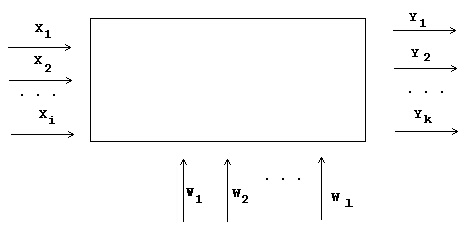
Основни обекти на моделирането са многофакторните обекти, представляващи обекти, които обединяват съвкупност от взаимозависими и взаимовлияещи си фактори (параметри). На фигура 1 е показана общата схема на един многофакторен обект.

2. Видове фактори. Различават се няколко вида фактори, от които зависи химичния експеримент.

Случайните фактори  W_l, са случайни въздействия върху многофакторния обект, чиито стойности са случайни числа и са напълно непредсказуеми. Тяхното въздействие е неконтролируемо и води до промяна на стойностите на изходните фактори. В редица случаи е възможно ограничаването на техните стойности в определен интервал.

Входните фактори X_i са факторите, които определят начина на функциониране на обекта. Техните стойности са случайни числа, но някои параметри на разпределението на тези числа (например тяхното математическо очакване) могат да се контролират или отчитат от експериментатора.

Изходните параметри Y_k съдържат сведения за качествените и количествени характеристики, описващи състоянието на обекта. Изходните параметри зависят в по-голяма или по-малка степен от входните фактори, като в редица случаи е възможно намирането на съответната регресионна зависимост. Например реакцията A + B а C е един многофакторен обект. Входни параметри са количествата на веществата A и B, температурата t, а също и количеството и вида на катализатора, ако реакцията е каталитична. Като изходен параметър се откроява количеството на веществото C, но за практически приложения на реакцията не по-малко важен изходен параметър е остатъчното съдържание на веществата A и B, т.е. чистотата на крайния продукт. При промишленото приложение на тази реакция важен изходен фактор е добивът на C. Случайни фактори са отклоненията на температурата и примесите във веществата A и C.

Най-общо, изходни параметри в химичния експеримент са добивът и чистотата на продуктите, производителността на даден химичен реактор, точността и възпроизводимостта, както и границата на откриване и границата на определяне на даден анализ. Входни параметри могат да бъдат концентрацията на реагиращите вещества, температурата и налягането, при които се извършва химичната реакция, вид и количество на катализатора, определени апаратурни параметри - ток, напрежение, потенциал.

Основна задача на математичното моделиране на експеримента е намирането на рагресионната зависимост на изходните параметри от входните фактори и определянето от нея на стойностите на входните фактори, за които изходните имат оптимални стойности. Когато изходният фактор е един, регресионната зависимост представлява една функция на този фактор от входните, ето защо този изходен фактор се нарича целева функция. При наличие на няколко изходни фактора от тях може да се състави математичен израз, който да представлява целевата функция, чийто оптимум ще се търси при оптимизирането. В горния пример за целева функция може да се приеме изразът C/(A+ B), който в благоприятния случай ще има максимум - висока концентрация C и ниски концентрации A и B.

3. Основни етапи на моделирането. За да се моделира даден обект, е необходимо да се определят факторите, които интересуват експериментатора и от тях да се състави целева функция. Следващи етапи са изборът на факторите, от които тя зависи и определяне на структурата на модела. След това се провеждат експериментите и се извършват изчисленията. Следва задължителният етап на статистическа проверка на модела и етапът на управление или оптимизиране на модела в зависимост от целите, поставени пред експериментатора. Последен етап от моделирането е проверка на модела върху реален обект и съответната интерпретация на резултатите.

1) Избор на целева функция. Видът на целевата функция е заложен от целите на експеримента и обикновено нейният избор е нееднозначен. Когато изходният параметър е само един, той се избира за целева функция, а при няколко, от тях се формира числов израз. Именно формирането на този израз е нееднозначно, но основно правило е той да зависи в най-голяма степен от най-важните изходни параметри. В редица случаи поради важността на всеки един от изходните фактори, се разкрива зависимостта на всеки един от тях от входните, т.е. разглежда се съвкупност от целеви функции.

2) Избор на входни фактори по вид и брой. В многофакторните обекти броят им обикновено е значителен. Колкото техният брой е по-голям, толкова повече експеримента са необходими за намирането на съответната регресионна зависимост. Затова е необходимо да се вземе под внимание, че не всички фактори имат еднакво влияние върху целевата функция. Изборът на най-важните, най-съществените факторите (тези, от които целевата функция най-силно зависи), се извършва по предварителни данни в литературата, чрез теоретични съображения или по аналогия с други модели. Много важно е между отделните фактори да няма корелационна зависимост, защото тя води до усложнения при обработване на опитните данни. Изборът на фактори е свързан и с големината на интервалите им на вариране, защото е възможно изборът на малък интервал на вариране да направи даден фактор несъществен. Освен това е възможна и несъвместимост между интервалите на вариране на редица фактори - несъвместимост, изразяваща се в повреда на опитната апаратура. Видът на регресионната зависимост, от своя страна, определя значимостта на даден фактор и тази информация задължително се използва за ново уточняване на избора на фактори.

3) Определяне на структурата на модела. Видът на регресионната зависимост зависи само от изходните и входните фактори, както и от интервалите на вариране на последните. Най-удобна за работа е линейната регресионна зависимост. Освен това нейните коефициенти имат пряк физически смисъл - големината на влиянието на съответните входни фактори. Както една крива може в определена точка да се замести със своята допирателна, така и всяка една регресия може да се приближи с линейна зависимост, като точността на това приближение силно ще зависи от големината на интервалите на вариране на входните параметри. Ето защо линейната регресия е най-разпространеният вид математичен модел.

Когато линейният модел е неадекватен, се използват регресионни полиноми от втора или трета степен, но с това се усложнява съответната математическа и статистическа обработка на данните и поради повечето на брой неизвестни коефициенти нараства и броят на необходимите експерименти.

Структурата на модела може да се обоснове теоретично или да се използват литературни данни. Но решаващи за нея са изводите, направени след статистическата обработка на резултатите - статистическата проверка за отличието от нула на коефициентите на регресия и проверката за адекватност (достоверност) на математичния модел.

4) Провеждане на експеримента. Експериментът се състои в събиране на данни за стойностите на целевата функция (изходните параметри) и на всички входни фактори. Задължително е неотчитаните входни фактори да заемат постоянни стойности. Той може да се проведе като пасивен експеримент, когато изследователят не се намесва в работата на обекта, а само отчита стойностите на факторите или като активен експеримент, когато стойностите на входните фактори се определят от изследователя. При пасивния вариант е затруднена съответната математическа обработка на данните и освен това влиянието на факторите, които не се отчитат (несъществените фактори) не е случайно, т.е. те не са случайни фактори. Това води до получаване на систематични грешки при определяне на регресионните коефициенти. Активният експеримент може така да се постави, че стойностите на входните фактори значително да облекчат математичната оброботка на данните. Също така редът на експериментите, включително и на техните повторения, се избира напълно случайно, което води до намаляване на неслучайния характер на неотчитаните фактори. Възможно е една част от входните фактори да се променя от експериментатора, а останалите да се отчитат пасивно - тогава се говори за смесен експеримент.

5) Обработка на данните. В този етап се извършва математическа обработка на събрания експериментален материал с цел определяне на коефициентите на регресия и изчисляване на необходимите величини за статистически анализ. Пресмятането им на ръка или с калкулатор е сложно и трудоемко, а също и нелишено от грешки. Ето защо е препоръчително използването на компютърни програми, например Excel или MathCAD.

6) Статистически анализ на модела. Задачата на настоящия етап се състои в статистическа оценка на стойностите на коефициентите на регресия и статистическа оценка на достоверността (адекватността) на съответното регресионно уравнение.

От получените интервални оценки на коефициентите на регресия могат да се направят изводи за тяхното статистическо отличие от нула. Ако някой от оценъчните интервали включва нулата в себе си, то съответният коефициент на регресия е неотличим от нула и в уравнението неговата стойност се записва равна на нула. От друга страна математичният модел (уравнението на регресия) може да се окаже статистически недостоверен. Това на практика означава, че избраната (например линейна) структура на модела не описва достатъчно добре опитните данни. В този случай е необходимо да се избере друга структура на модела (например регресия от втора степен), с която да бъдат обработени данните. Това означава повтаряне отново на етапи 2, 3, 4 и 5 или на част от тях до получаване на статистически достоверен модел.

7) Управление и оптимизиране на обекта. Създаването на математичния модел не е крайната цел на експериментатора. В зависимост от поставената цел, той може да се използва за управлението на реалния обект или за неговото оптимизиране.

Задача на управлението може да бъде поддържането на определени стойности на изходните параметри или тяхната промяна в дадени моменти от времето. Тя се решава на базата на математичния модел, посредством математични пресмятания. Обикновено на даден набор от изходните параметри съответстват няколко или безкраен брой съвкупности на входните фактори. Ето защо по-сложна задача на управлението може да бъде изборът на такава съвкупност от входни фактори, която ще осигури по-икономично функциониране на реалния обект.

Математичният модел може да се използва и за оптимизиране на процесите в реалния обект. Обикновено се оптимизират стойностите на целевата функция, като се търси нейният максимум или минимум. Уравненията на регресия са удобни за оптимизиране, тъй като отпадането на един или няколко входни или изходни фактора не променят модела и той пак може да се използва. Например ако вече не се следи стойността на един от изходните фактори, не е необходимо да се разглежда и съответното регресионно уравнение, описващо зависимостта му от входните параметри, докато останалите уравнения са същите. Ако пък даден входен фактор престане да се изменя, то във всички регресионни уравнения ще бъде поставена неговата постоянна стойност, при което те запазват своята адекватност. Както ще бъде показано в следващите материали, при другите методи на оптимизация, ще са необходими нови експерименти в тези два случая.

8) Проверка на модела и интерпретация на резултатите. В етапи 1) - 7) са възможни редица груби експериментални и изчислителни грешки, както и неправилен избор на факторите. Ето защо е целесъобразно математичният модел да се провери върху реалния обект. За тази цел се провеждат допълнителни експерименти, при стойности на входните параметри, различни от тези, използвани при създаване на модела. Съответните стойности на входните фактори се заместват в регресионните уравнения и получените числови резултати се сравняват статистически с експерименталните. Когато стойностите на входните параметри при проверката лежат в областите, в които те са изменяни при създаване на модела, се извършва проверка за интерполация по модела, а когато те лежат извън тези области - проверка за екстраполация по модела.

Необходимо е да се отбележи, че интерпретирането на резултатите е изцяло неформализиран етап и изисква съобразителност, внимание и в известна степен въображение. Тук могат да се включат всички теоретични знания на експериментатора, аналогии с други модели, сравняването на регресионната зависимост с физикохимичните закони и др. В редица случаи внимателният анализ на математичния модел разкрива по-общи теоретични зависимости, които могат да се обяснят с (физико)химичната теория и които спомагат за разкриване на химизма на процесите в реалния обект.

1. Футеков Л., Пенчев П., "Теория на експеримента", Пловдив, Изд. ПУ, 1992, 1998.

Автор: Пламен Пенчев, Ph.D.