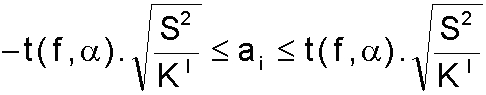 (7.7)
(7.7)С този материал започнахме една поредица за приложение на хемометриката в химията. В тази лекция ще продължим разглеждането на моделирането на химичния експеримент, което започнахме в предишната лекция.
Идеята на този експеримент може да се подскаже от следните разсъждения. За да се определи влиянието на даден входен фактор върху целевата функция, е необходимо да се проведат два експеримента, единият при една стойност на този фактор, а другият при друга стойност, т.е. два експеримента при две нива на входния фактор - долно ниво и горно ниво. Аналогично влиянието на всеки един от факторите се разкрива по този начин, при което се използват 2N на брой експеримента, където N е броят на входните параметри. Всъщност за всеки набор на входните фактори е необходимо извършването на няколко опита (наричани повторения или паралели) с цел по-точна оценка на истинската стойност на целевата функция. След усредняване на стойностите на целевите функции от повторенията се получават 2N независими резултата, от които могат да бъдат изчислени не повече от 2N коефициента на регресионната зависимост.
Поради тази причина, както и за улеснение при пресмятанията, регресионната зависимост е удобно да се избере от вида
Y = a0 + SaiXi + Sai,jXiXj + ... + a1,2..NX1X2...XN, (7.1)
където Xi, i = 1 .. N, са входните фактори, Y е целевата функция, а коефициентите на регресия a0, a1, ... a1,2..N са 2N на брой. Например за три фактора, регресионното уравнение ще изглежда по следния начин:
Y = a0 + a1X1 + a2X2 + a3X3 + a1,2X1X2+ a1,3X1X3 + a2,3X2X3 + a1,2,3X1X2X3 (7.1a)
Тези данни са достатъчни за всеки математик, който иска да изчисли коефициентите на регресия. От 2N-те независими резултата, могат да бъдат написани 2N линейни уравнения с неизвестни a0, a1, ... a1,2..N, с коефициенти пред неизвестните - 1, X1, ... X1X2...XN и свободни членове - Y (във всяко уравнение Y и Xi приемат конкретните експериментални стойности). Но с цел улеснения при пресмятанията и практическото използване на модела химиците работят по друг начин.
1. Пълен факторен експеримент. За всеки един от входните фактори Хi се избира интервал на вариране (Хimax,Хimin), чиито граници се наричат долно и горно ниво на фактора. Средата на интервала Хi0 = (Хimax + Хimin)/2 се нарича основно ниво на съответния фактор. Тъй като входните фактори имат различна размерност и различни интервали на вариране, то големината на коефициентите в (7.1) не може да даде относителното влияние на всеки един от параметрите върху целевата функция. Ето защо следващата стъпка е привеждането на стойностите на входните параметри в безразмерни числа Zi по формулата:
Zi = (Хi - Хi0)/(Хimax - Хi0) (7.2)
Числата Zi се наричат кодирани стойности на факторите. Ако се заместят стойностите на горно и долно ниво на съответните параметри в (7.2), за кодираната стойност на долно ниво ще се получи -1, а за тази на горно ниво - +1, т.е. Zimin = -1 и Zimax = +1.
Ако математичният модел има два входни параметъра съответното регресионно уравнение, което дава зависимостта на некодираната целева функция от кодираните фактори, е следното:
Y = a0 + a1Z1 + a2Z2 + a1,2Z1Z2 (7.3)
Вижда се, че всички коефициенти
на регресия са с размерността на целевата
функция. Кодираните стойности, при които
ще се провеждат 22
= 4 експеримента, ще
са следните:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
За всеки един от четирите набора на входните параметри се провеждат няколко паралелни измервания на целевата функция (паралели, повторения). Намират се техните средни стойности Yj, където j е номерът на експеримента. Например за два фактора, ако се провеждат пет повторения са необходими общо 4х5 = 20 измервания на целевата функция.
При три фактора, регресионно уравнение ще се дава с формулата:
Y = a0 + a1Z1 + a2Z2 + a3Z3 + a1,2Z1Z2 + a1,3Z1Z3 + a2,3Z2Z3 + a1,2,3Z1Z2Z3 (7.4)
а кодираните стойности,
при които ще се провеждат 23
= 8 експеримента, ще
са следните:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тази таблица (както и предишната) от кодирани стойности на входните параметри се нарича план-матрица на експеримента. Тя може да се запише по различни начини, но най-удобният е следният: за първия фактор първата половина стойности са -1, а втората половина +1. За втория фактор първата четвърт са -1, втората четвърт +1, третата -1 и последната +1. За третия параметър първата осма са -1, и т.н. За последния фактор кодираните стойности се променят от експеримент на експеримент. Могат да съществуват различни начини на подредбата на кодирането на експериментите, но важно е да няма повторения в набора от входни фактори.
План-матрицата притежава свойства, които се използват за изчисляване на коефициентите на регресия. Тези свойства лесно могат да се проверят чрез използване на стойностите на Zi от двете таблици по-горе. С Zij се означават кодираните стойности на параметрите, където i е номерът на съответния фактор (номерът на стълба), а j - номерът на експеримента (реда). Сумите по-долу се сумират по j от 1 до K, където K е броят на независимите експерименти: K = 2N.
1) Сумата от кодираните стойности на всеки един от факторите е нула, т.е. сумата на числата във всеки стълб е равна на нула.
S Zij = 0
2) Сумата от квадратите на числата във всеки стълб е равна на броя на експериментите К; К = 2N. Причината е, че (Zij)2 = 1.
S (Zij)2 = К
3) Всеки два стълба са ортогонални, т.е. сумата на произведението на числата на всеки два стълба е нула (символът =/= означава различно).
S ZijZkj = 0, за j =/= k и очевидно (вижте свойство 2) е равно на 1 за j = k;
4) Сумата от взаимното произведение на повече от два стълба е равно на нула, например това на три стълба.
S ZijZkjZlj = 0, за j =/= k =/= l.
Чрез използването на свойства 1) - 4) могат да се получат формулите за оценките на коефициентите на регресията (7.4), които се означават с b0, b1, ... b1,2,..N.
b0 = S Yj/K (7.5a)
bi = S YjZij/K; i = 1 ... N (7.5b)
bi,k = S YjZijZkj/K; i,k = 1 ... N (7.5c)
Сумира се по номера на експеримента j от 1 до K, където K е броят на независимите експерименти: K = 2N. С Yj се означава средната стойност от измерените значения на целевата функция при стойности на входните параметри, дадени в ред номер j.
2. Статистическа обработка на резултатите. Тъй като измерените стойности на целевата функция са случайни величини и следователно случайни величини са и коефициентите (7.5), е необходим статистически анализ, за да се приемат резултатите.
Първо се проверява хипотезата за еднакви възпроизводимости на отделните експерименти, т.е. за еднородност (статистическа неотличимост) на съответните дисперсии. За всеки набор от входни параметри се провеждат няколко измервания на целевата функция, които се характеризират със своето стандартно отклонение. Ако Ymj е стойността на целевата функция при m-тото повторение на j-я експеримент и броят на повторенията е M, то средната стойност и стандартното отклонение на целевата функция при тези повторение се изчисляват с формулите (сумира по m се от 1 до M):
`Yj = S Ymj/M (7.6a)
Sj2 = S (Ymj -`Yj)2/(M-1) (7.6b)
Оценките на коефициентите на регресия се изчисляват по формули (7.5), само ако между всички Sj няма статистическа разлика, т.е. възпроизводимостите на различните експерименти са еднакви. При еднакъв брой паралели M във всички експерименти хипотезата за равенство между Sj може да се провери с критерия на Фишер. За тази цел се изчислява отношението
Fkr = Smax2/Smin2,
където Smax е най-голямото стандартно отклонение, а Smin най-малкото от всички Sj. Избира се ниво на значимост a и от таблица на интегралните граници на F-разпределението за степените свобода f1 = M - 1 и f2 = M - 1 се намират интегралните граници F(f1,f2, a) = F(f2,f1, a) - в случая те са едни и същи, защото f1 = f2. При 1/F(f2,f1, a) < Fкр < F(f1,f2, a), възпроизводимостите на всички експерименти са еднакви. Ако не са изпълнени двете неравенства, възпроизводимостите не са еднакви. В този случай е необходимо провеждането на част от експериментите, за да се провери дали тази разлика във възпроизводимостите не се дължи на груби експериментални грешки или е физически присъща на съответните експерименти. Проверката за еднородност на дисперсиите на отделните експерименти може да се извърши с критерия на Кохрън или с критерия на Бартлет.
Следва проверката за статистическата значимост (статистическото отличие от нула) на регресионните коефициенти. За тази цел се извършва тяхното интервално оценяване, чрез теста на Стюдънт. Ако нулата принадлежи на даден оценяващ интервал, то съответният регресионен коефициент е статистически неотличим от нула и той се приема за равен на нула в уравнението (7.3), съответно (7.4). В противен случай той е статистически значим и в уравнение (7.3), съответно (7.4) присъства неговата експериментална стойност.
Когато броят на повторенията на всички експерименти са равни помежду си и съответните им възпроизводимости са еднакви, интервалната оценка на коефициентите ai (съответно ai,k и a1,2,3) се дава с уравнението
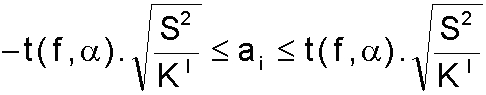 (7.7)
(7.7)където t(f, a) е интегралната граница на t-разпределението при ниво на значимост a и степени свободаf = К(M - 1); К е броят на експериментите, M е броят на повторенията на всеки един експеримент, а К' = КM е броят на всички опити. Стандартното отклонение S е оценка за дисперсията на отделните експерименти (само при еднаквата им възпроизводимост) и е равно на:
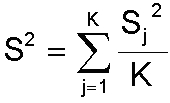 (7.8)
(7.8)
Тъй като във всички формули (7.5) присъстват членовете Yj в числителя и N в знаменателя, а изразите от вида Zi или ZiZk или ZiZkZl са равни на +1 или -1 и като се имат предвид свойствата на дисперсията, интервалната оценка (7.7) се отнася за всички коефициенти на регресия - ai, ai,l и a1,2,3 и т.н.
Адекватността на модела (7.4) се проверява с критерия на Фишер. За тази цел се изчислява стандартното отклонение (на адекватност) Sad, което е равно на:
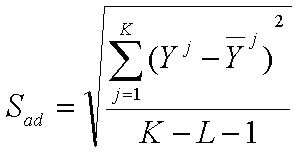
Fкр = Sad2/S2,
където S е стандартното отклонение (7.8) на експериментите. За степени свобода fad= K - L - 1 и f = К(M - 1) и избрано ниво на значимост a се намира интегралната граница F(fad, f, a) на F-разпределението. Ако Fкр< F(fad, f, a), моделът е адекватен, а при Fкр> F(fad, f, a) е неадекватен.
Литература
1. Футеков Л., Пенчев П., "Теория на експеримента", Пловдив, Изд. ПУ, 1992, 1998.
Автор: Пламен Пенчев, Ph.D.
[ това е материал от брой 27 от февруари 2009 г. на списание "Коснос" www.kosnos.com ]