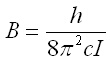Задача 1. В ротационния спектър на ¹H³⁵Cl се наблюдават следните линии за преходите j"иj’:

положение на линията: 83.32   104.13   124.73   145.37   165.89    [сm^-1]
преход:               4и3     5и4     6и5      7и6     8и7

Пресметнете ротационната константа B и разстоянието между атомите r_H-Cl.

Решение:

Вълновите числа на тези пет прехода удовлетворяват уравнение (13) от тази лекция,

Реално това уравнение се удовлетворява пет пъти за стойности на j", равни на 3, 4, 5, 6 и 7. Това на практика са пет уравнения с две неизвестни - B и D. Коефициентите пред неизвестните са 2(j"+1) и -4(j"+1)³, съответно за j", равни на 3, 4, 5, 6 и 7.  Това е една преопределена система от пет уравнения с две неизвестни, във вида AX = B, която се решава чрез намиране на обобщената обратна матрица на A, която е равна на (A^TA)^-1A^T.  Ако умножим уравнението AX = B отляво с обобщената обратна матрица на A получаваме (I е единичната матрица)

(A^TA)^-1A^TAX = (A^TA)^-1A^TB = IB = B,

т.е. матрицата на неизвестните X е равна на (A^TA)^-1A^TB.

Точно това е направено във Excel файла rotat.xls, където матрицата  е разположена в клетки B11:C15: тя е изчислена с 2(j"+1) и -4(j"+1)³, при заместване на j" с 3, 4, 5, 6 и 7. Матрицата B е разположена в клетки D11:D15. Съответно за константите B и D се получава (в сm^-1) 10.43413575 и 0.000517396 - клетки B33:B34. Т.е. B = 10.434сm^-1 и D = 0.000517сm^-1.

Тъй като ротационната константа B е свързана с инерчния момент I с уравнение (8) от тази лекция,

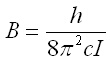            (1)

Тогава за междуядреното разстояние r се получава

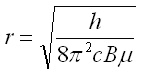
Съответните изчисления са проведени в клетка I34 на Excel файла rotat.xls, при което се получава r = 1.28907x10^-10 m. Това е 1.289 Ангщрьома (1 Ang = 1x10^-10 m), което е близко до експерименталната стойност 1.274, която е дадена в справочника [2] - вижте и тази страница; същото разстояние е дадено и в Енциклопедия Уикипедия - вижте тази страница. Разликата между намереното разстояние от ротационния спектър и експерименталното е около 1%, което е добро съвпадение.

При изчисленията по-горе, обърнете внимание, че Джаулът J се изразява чрез килограм, метър и секунда по следния начин J = kg m² s^-2, при което мерните единици в корена дават

Задача 2. Междуатомните разстояния в молекулите на ¹H³⁵Clи ¹H³⁷Cl са приблизително равни. Използувайки резултатите от задача 1 пресметнете ротационната константа B за ¹H³⁷Cl.

Решение: Разликата между двете ротационни константи ще се дължи на инерчния момент, по-точно на приведената маса m. По уравнение (1) по-горе константите са

B_1H35Cl = h/(8p²cI_1H35Cl) и  B_1H35Cl = h/(8p²cI_1H37Cl)

т.е.  B_1H35Cl/B_1H35Cl = I_1H35Cl/I_1H37Cl,

или

B_1H35Cl = B_1H35ClI_1H35Cl/I_1H37Cl = B_1H35Clm_1H35Clr²/m_1H37Clr² = B_1H35Cl1m_H35Cl/m_1H37Cl

Отношението m_H35Cl/m_1H37Clе равно на [1x35/(1+35)]/1x37/(1+37) = 35/37*38/36 = 0.9985, при което получаваме, че

B_1H35Cl = B_1H35Cl1m_H35Cl/m_1H37Cl = B_1H35Cl1m_H35Cl/m_1H37C = 10.434 сm^-1 x 0.9985 = 10.418 сm^-1

Задача 3.  Разликата между честотите на първите две линии от задача 1 е 20.81 сm^-1, а между последните две - 20.52 сm^-1. Защо?

Решение:

Причината за тази разлика е наличието на константа на центробежно разтегляне, D, която както видяхме от решението на задача 1 е D = 0.000517сm^-1. Ако се замести нейната стойност в уравнение (13) от тази лекция ще наблюдаваме гореспоменатото намаление между линиите.

1.  Г. Андреев. Молекулна спектроскопия, Изд. ПУ “П. Хилендарски”, Пловдив, 1999.

2. James G. Speight; Lange's Handbook of Chemistry.McGraw-Hill, New York, 2005.

3. К.-П. Хъюбнер, Г. Герцберг; Константы двуатомный молекул. Мир, Москва, 1984.

Автор: д-р Пламен Пенчев