Въртене на многоатомни молекули
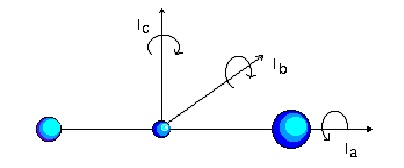
1. Видове ротатори. Ротационните спектри на многоатомните молекули са много сложни поради факта, че въртенето може да се извършва по трите молекулни оси, при което съответните им моменти на инерция могат да бъдат различни. Въз основа на отношението на инерчните моменти всяка многоатомна молекула може да се причисли към един от следните типове въртящи се молекули:
1. Сферичен ротатор (Ia = Ib = Ic). Примери: CH4, SF6, CCl4.
2. Симетричен ротатор (Ia = Ib =/= Ic). Примери: C6H6, CHCl3, C2H6, H2C=C=CH2, NH3.
3. Линеен ротатор (Ia = 0; Ib = Ic). Примери: CO2, HCN, HC@CH.
4. Асиметричен ротатор (Ia =/= Ib =/= Ic). Примери: H2O, C3H8.
Линейният ротатор представлява всъщност частен случай на симетричен ротатор.

Моментите на инерция на линейните многоатомни молекули се изчисляват по същото уравнение както за двуатомните, поради което те притежават поредица от енергетични нива, положението на които се определя от уравнение (12) от предишния материал. При такива молекули, притежаващи диполен момент, се наблюдават спектри, линиите в които отстоят на разстояние 2B една от друга, коригирани със съответните стойности на центробежното разтегляне - фигура 6 от предишния материал. Тъй като моментът на инерция на многоатомните молекули е значително по-голям, отколкото при двуатомните (ротационната константа В и инерчния момент I са в обратна зависимост), стойностите на ротационните константи при тях ще бъдат по-малки; те са обикновенно под 1cm-1.
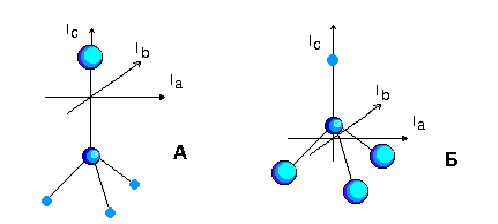
Молекулите, спадащи към типа симетричен ротатор, притежават три различни от нула инерчни момента, два от които са равни помежду си. Различават се два случая - вижте фигура 2.
1. Ia
= Ib > Ic,
наречени удължена сфера (prolate), например CH3Cl.
2. Ia
= Ib < Ic,
наречени сплесната сфера (oblate), например CHCl3.
При този тип молекули съществуват две посоки на въртене, които са свързани с поглъщане или излъчване на енергия - по главната ос С-Cl (за първия случай) и перпендикулярната на нея. За описание на тези две въртения са нужни две квантови числа - едно за Ic и едно за Ia или Ib. От математична гледна точка обаче е удобно да се въведе едно квантово число, което да съответствува на сумата от моментите по двете оси. Този тотален ъглов момент се означава с J; J може да приема произволни стойности. Ъгловия момент по Ic се означава обикновено с K. Да отбележим, че K не може да заеме стойности по-големи от тези на тоталния ъглов момент J. Освен това K може да заема както положителни, така и отрицателни стойности, съотствествуващи на въртене по посока на часовата стрелка и срещу нея. Следователно квантовото число K може да заема 2J+1 стойности:
K = J, J-1, J-2,...0,...-(J-2), -(J-1), -J (1)
При решаване уравнението на Шрьодингер за молекулите симетричен ротатор се получава израза:
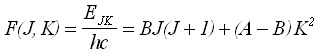 (2)
(2)
където:
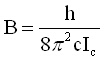 ;
; 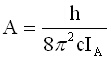 (3)
(3)Ако К има голяма стойност, близка до J, по-голямата част от молекулното въртене се извършва около оста на симетрия. За всяка стойност на К > 0 ротационните нива са двукратно изродени. Ако К = 0 цялото въртене представлява едно премятане, като енергията зависи или от Ia или от Ib. Както се вижда от (2), енергията зависи от К2, поради което посоката на въртене е без значение.
В таблица 1 са сравнени данните от изчислените и опитно измерени стойности на честотите на линиите в ротационния спектър на CH3F. Вижда се изключителната прецизност, с която могат да се измерват спектрите в микровълновата спектроскопия.
Таблица 1. Изчислените и опитно
измерени стойности на честотите на линиите в ротационния спектър на CH3F.
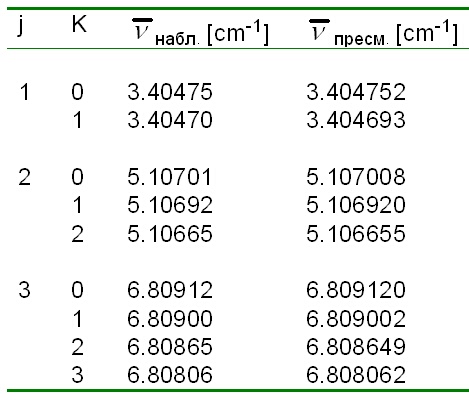
Въз основа на тези данни могат да се пресметнат дължините на връзките, валентните ъгли и съответните им силови константи, диполният момент, изотопното съдържание и др.
Ротационните спектри на молекули от типа асиметричен ротатор са много сложни за интерпретиране. Да припомним, че молекули от типа сферичен ротатор не притежават диполен момент и ротационни спектри.
2. Апаратура и начин на работа. Спектрите на въртене на молекулите се регистрират за проби намиращи се в разредено газообразно състояние; достатъчно е налягане от 10-2-10-3 torr. Ето защо на изследване могат да бъдат подложени и редица вещества, които са течни или твърди при обикновени условия. При повишаване на налягането, поради увеличаване броя на сблъсканията между молекулите и появата на междумолекулни взаимодействия, структурата на спектрите на ротация се изменя - ивиците се разширяват и припокриват, което затруднява или прави интерпретацията им невъзможна.
Като източник на микровълни се използува клистронова електронна лампа, която излъчва в много тесен честотен интервал практически "монохроматично". Сканирането се извършва чрез електрониката на прибора.
Като проводник на микровълните се използува медна или сребърна тръба, най-често с правоъгълно вътрешно сечение. Тъй като въздухът има значително поглъщане, системата се вакуумира. Приемникът на микровълново лъчене представлява обикновен суперхетеродинен приемник. Сигналът се усилва електронно и се изобразява на осцилоскоп.
Задачи
Задача 1. В ротационния спектър на 1H35Cl се наблюдават следните линии за преходите J"иJ’:
положение на линията: 83.32
104.13 124.73 145.37 165.89
[сm-1]
преход:
4и3
5и4
6и5
7и6
8и7
Пресметнете ротационната константа B, константа на центробежно разтегляне D и разстоянието между атомите rH-Cl.
Отговор: B = 10.434 сm-1, D = 0.000517сm-1 и rH-Cl = 1.289x10-10 m.
Вижте решението на задача 1.
Задача 2. Междуатомните разстояния в молекулите на 1H35Cl и 1H37Cl са приблизително равни. Използувайки резултатите от задача 1 пресметнете ротационната константа B за 1H37Cl.
Вижте решението на задача 2.
Отговор: B1H37Cl = 10.418 сm-1.
Задача 3. Разликата между честотите на първите две линии от задача 1 е 20.81 сm-1, а между последните две - 20.52 сm-1. Защо?
Вижте решението на задача 3.
Литература
1. Г. Андреев. Молекулна спектроскопия, Изд. ПУ “П. Хилендарски”, Пловдив, 1999.
Автор: проф. дхн Георги Андреев