Въртене на двуатомна молекула
( съдържание )
Изучаването на въртеливото движение на молекулите се извършва чрез измерване на техните спектри в далечната инфрачервена и в микровълновата област на електомагнитния спектър (под 100 cm-1). Задължително условие за наблюдаване на спектър на въртене е молекулата да притежава диполен момент. Това може да се илюстрира (на основата на класическата електродинамика) с въртенето на молекула флуороводород.
Поради високата електроотрицателност на флуорния атом, последният изтегля електронната двойка, образуваща връзката Н-F. В резултат флуорният атом се оказва натоварен с частичен отрицателен заряд, водородният с частичен положителен, а молекулата като цяло има постоянен електричен диполен момент. Ако НF извършва чисто въртеливо движение (т.е. центърът на масите не се премества), диполният момент ще се променя периодично в дадено направление с честотата на въртене. От тези класически разглеждания следва, че при въртенето на НF може да се излъчи или погълне електромагнитно лъчение (от микровълновата oбласт на спектъра) с честота равна на ротационната. Следователно, молекули които притежават диполен момент са "микровълново активни", докато онези, които нямат диполен момент са "микровълново неактивни"; такива са например хомоядрените двуатомни молекули Н2, О2, Cl2 , молекулите с център на симетрия - бензена и въглеродния диоксид и др.
Изясняването на физическата природа на явлението въртене ще извършим за най-простия случай на молекула - хетероядрена двуатомна. При това, разглежданията водят до един опростен модел на двуатомна молекула, известен като твърд ротатор.
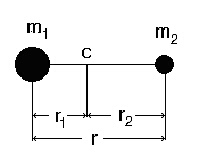
1. Класическо разглеждане на твърдия ротатор. Двуатомната молекула, може да бъде представена като две материални точки с маси m1 и m2, закрепени чрез твърда, безтегловна пръчка на разстояние r една от друга. Основа за такова представяне е фактът, че почти цялата маса на атомите е съсредоточена в ядрата, чиито размери (~10-14 m) са с около четири порядъка по-малки от междуядреното разстояние (~10-10 m).

Означавайки разстоянието на материалните точки до центъра на масите C с r1 и r2 съответно, може да се запише:
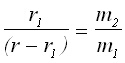
Следователно:
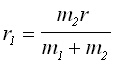 (1a)
(1a)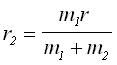 (1b)
(1b)Кинетичната енергия на твърдия ротатор Er зависи, съгласно класическата механика, от момента на инерция I и от ъгловата скорост w:
Er = Iw2/2 (2)
където I = m1r12 + m2r22, а w = 2pnr ; nr - честотата на въртене на твърдия ротатор.
Заместването на получените в (1a) и (1b) стойности за r1 и r2 в израза за I води до следния израз за момента на инерция:
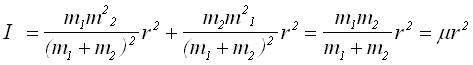 (3)
(3)
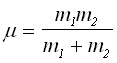 (4)
(4)Величината m се нарича приведена маса (reduced mass).
Оказва се, че въртенето на твърдия ротатор е еквивалентно на въртене на материална точка с приведена маса m на разстояние r от оста на въртене, което е равно на междуядреното - вижте фигура 2.
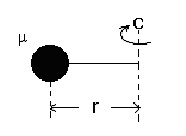
Заместването на получената стойност за инерчния момент във формулата за енергията (2) показва, че съгласно класическите представи твърдият ротатор може да заеме произволни стойности на енергията Er.
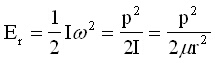 (5)
(5)2. Квантова механика на твърдия ротатор. За молекулите като микросистеми са в сила квантовомеханичните закони, според които стойността на квадрата на момента на импулса на въртене и проекцията на момента на импулса в дадено направление се квантуват. При съставяне на уравнението на Шрьодингер за енергията на твърдия ротатор се получава следният израз:
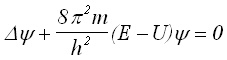
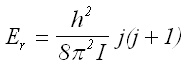 [J] (6)
[J] (6)
за които ротационно квантово число j = 0,1,2... От (6)следва, че се получава серия от дискретни нива, т.е. енергията се квантува, при това с нарастване на j енергията се увеличава в квадрат.
Сравняването на формулите (5) и (6) води до израза:
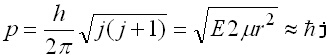
Следователно ротационното квантово число дава приблизително импулса в единици h/2p, тъй като корен от [j(j+1)] можем да приемем, че е равно на j за големи стойности на j.
Енергията на нивата се представя в спектроскопията в единици вълнови числа `n, при което се получават величини, наречени термове. За ротационните термове F(j) на твърдия ротатор сe получава:
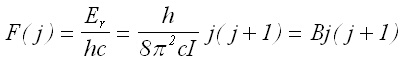 (7)
(7)
където
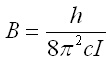 (8)
(8)
се нарича ротационна константа.
От (8) следва, че с нарастване на масата на въртящата се молекула ротационната константа В ще намалява. Експерименталните данни потвърждават този извод: В(Н2) = 60.809 cm-1; В(D2) = 30.429 cm-1; В(HCl) = 10.591 cm-1; В(J2) = 0.0374 cm-1. (Данните за В на хомоядрените молекули са получени чрез Раман-спектроскопия)
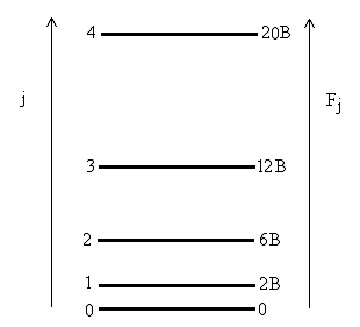
Давайки на ротационното квантово число j последователно разрешените цели стойности, за ротационните термове F(j) се получава поредица от нива с нарастващи енергии. При j = 0, F(j) = 0, което ще рече, че молекула, намираща се в нулево ротационно състояние не се върти. При даване на j стойности 1, 2, 3,... се получава система от енергетични нива, разстоянието между които нараства при всяка следваща стойност на j - вижте фигура 3.
Съгласно изложеното по-горе, поглъщане или излъчване на подходящ квант енергия от определена молекула ще се наблюдава само ако последната притежава собствен електричен диполен момент, различен от нула. Подборното правило за твърдия ротатор, получено при решаване уравнението на Шрьодингер е следното: разрешени са само преходи, които се извършват с промяна на ротационното квантово число с 1, т.е. Dj = ±1 (при Dj = +1 се извършва поглъщане на фотон, при Dj = -1 - излъчване). На всеки от тези преходи ще съответствува спектрална линия, вълновото число на която може да бъде пресметнато въз основа на разликата между ротационните термове. Използувайки възприетия начин на означаване на енергетичните нива - горното с прим, а долното със секонд, за вълновото число `n на един излъчен квант j' = j" + 1 се получава:
= 2B(j" + 1)
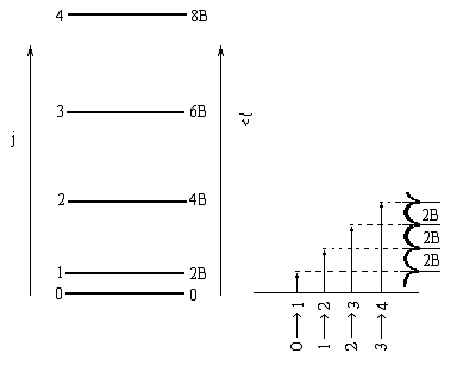
За стойности на j = 0,1,2... се получава серия равноотстоящи линии, разликата между които е 2B - вижте таблица 1 и фигура 4.
Taблица.1. Ротационни термове и честоти на въртене на твърд ротатор при различни стойности на ротационното квантово число j.

3. Интензитет на линиите. Възниква въпросът, какъв ще бъде относителният интензитет на линиите в ротационния спектър на една двуатомна молекула, разглеждана като твърд ротатор.
Интензитетът на ивиците зависи от вероятността за преход и отношението на населеностите на съответните енергетични нива съгласно закона на Болцман. Прецизни изчисления са показали, че вероятността за преход от всички енергетични нива е с добро приближение еднаква. С други думи, еднакво вероятно е да се извърши както преход между ротационни нива от j = 0иj = 1, така и между j = 1иj = 2, j = 2иj = 3 и т.н.
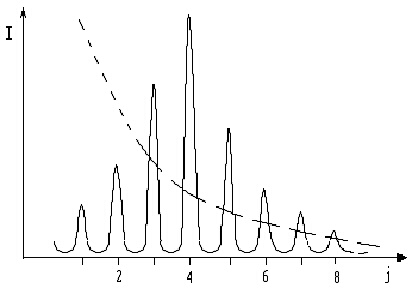
Поради незначителните разлики между ротационните енергетични нива (вижте фигура 5), при стайна температура голяма част от възбудените нива на двуатомните молекули са вече заселени под влияние на термичната енергия. Например за молекула, притежаваща ротационна константа В = 3 см-1, отношението на населеностите между първото възбудено и основното състояние е около 0.9, но спада бързо с нарастване на j. В такъв случай би следвало да се очаква, че интензитетът на линиите ще намалява последователно от (j = 0 иj = 1), (j = 1 иj = 2), (j = 2 иj = 3) ... (пунктирна линия на фигура 5). На практика обаче, в експериментално измерените спектри, интензитетът на линиите отначало расте минавайки през максимум, а след това намалява. На фигура 5 е представена зависимостта на интензитета на линиите като функция от ротационното квантово число.
Причина за такова разпределение на интензитетите е израждане на енергетичните състояния. Квантовомеханичните разглеждания на ъгловия момент показват, че проекцията на ъгловия момент К приема (2j+1) стойности (-j, -(j-1), ... 0, 1, ... j), т.е. всяко ротационно енергетично ниво е (2j+1) пъти изродено. Когато j = 1 израждането е трикратно (т.е. има три ориентации на вектора на ротационния ъглов момент), при j = 2 израждането е петкратно и т.н. Следователно, макар с нарастване на ротационното квантово число j населеностите да намаляват експоненциално, броят на изродените нива бързо расте. Отношението на населеностите в ротационните спектри се дава с израза:
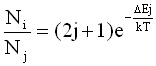 (10)
(10)
Диференцирането на този израз показва, че населеността има максимум при стойност на j, която се дава с израза:
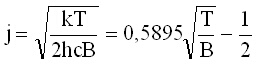 (11)
(11)
което е в съгласие с опитните данни.
4. Еластичен ротатор. Данните от експеримента показват, че с нарастване на номера на линията в ротационните спектри на двуатомните молекули, разстоянието между тях постепенно намалява. Това сближаване на линиите се обяснява с разтегляне на молекулата поради нарастване на центробежните сили с увеличаване на ротационното квантово число.
При решаване уравнението на Шрьодингер за еластичния ротатор, във формулата за енергията (7) се включва още един член, отчитащ центробежното разтегляне:
където D се нарича константа на центробежно разтегляне. Стойността на е D е много по-малка от единица - вижте решението на задача 1 от следващия материал, където за молекулата на 1H35Cl се получава, че B = 10.434сm-1 и D = 0.000517сm-1.
Подборното правило за нетвърдия ротатор не се променя, то остава Dj = ±1. Тогава за един излъчвателен преход F(j') - F(j") можем да запишем:
= B[(j"+1)(j"+2) - j"(j"+1)] - D[(j"+1)2(j"+2)2 - j"2(j"+1)2] = (13)
= 2B(j"+1) - 4D(j"+1)3 [сm-1]
От (13) следва, че еластичният ротатор се различава от твърдия по отместването на всяка от линиите към по-ниските честоти. На фигура 6 са сравнени енергетичните нива и ротационни спектри на твърдия и еластичния ротатори:
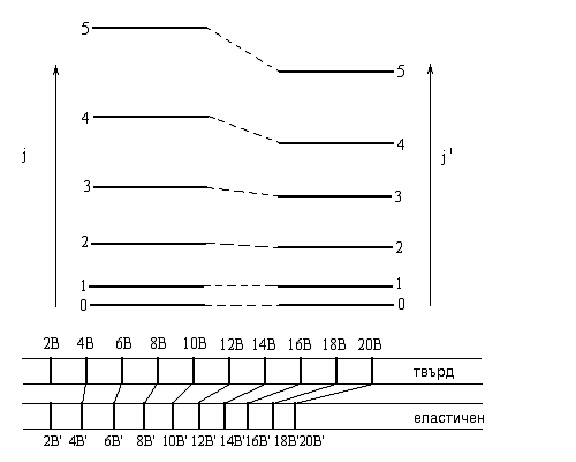
С помощта на модела на еластичния ротатор се получават данни за геометрията на двуатомните молекули: инерчен момент, атомни маси и др. Пресметнатите стойности са в много добро съгласие с опитно получените.
Литература
1. Г. Андреев. Молекулна спектроскопия, Изд. ПУ “П. Хилендарски”, Пловдив, 1999.
Автор: проф. дхн Георги Андреев