The Encoding is Cyrrilic (Windows - 1251)
                               Страниците с формули най-добре се четат с Майкрософт Интернет Браузър: на другите браузъри не излизат гръцките букви!

c2-разпределение

( съдържание )

С този материал започнахме една поредица за приложение на статистиката в химията. Материалът може да се използва не само от химици, а от всички, които се занимават с обработка на експериментални резултати.

1. c2-разпределение с n степени на свобода. Това е разпределение на случайна величина c2n = У12 + У22 + ... + Уn2, където Уk, k = 1 ....n са случайни величини, разпределени стандартно (нормално с m  = 0 и s2  = 1) и са независими. Цялото число n се нарича степени на свобода и обикновено се означава с f .

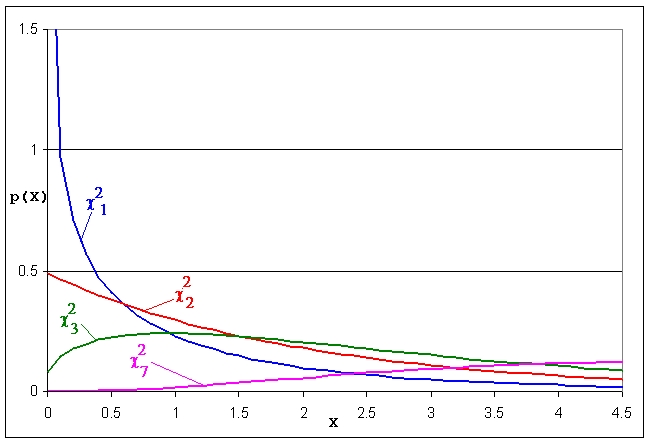
Плътността на разпределението се дава с уравнение (1)  и е представена на фигура 1. Тя е с несиметрична форма, която силно зависи от степените свобода  n. При голям брой степени свобода c2 разпределението преминава в нормално разпределение.

                 м {1/[2n/2 G(n/2)]} [Xn/2-1 e-X/2], за X > 0
          р(Х) = н                                                      (1)
                 о 0, за Х < 0

където  Г() е така наречената гама функция.

Фигура 1. Плътност на c2-разпределението при няколко степени на свобода, f = 1, f = 2, f = 3, f = 7.

Ясно се вижда от формула (1), че плътността на c2-разпределението е тъждествено равна на нула при Х < 0.

Ако`Х е средната стойност на N измервания, а s2 е дисперсията на разпределението (генералната съвкупност) на тези измервания, то случайната величина

S(Хk - `Х)2/s2 = (N - 1) S2 / s2

е  c2 разпределена с N-1 степени свобода.

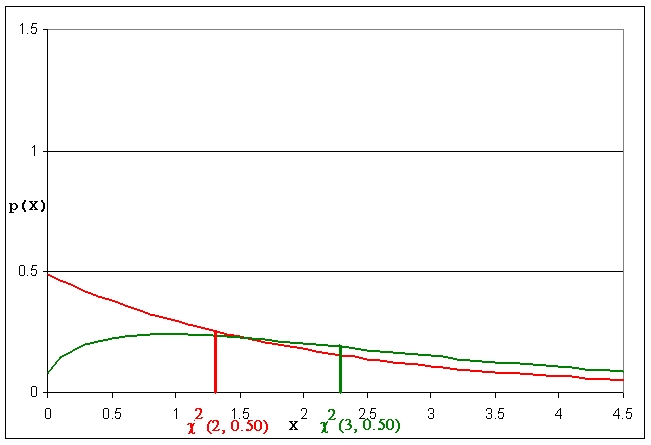
В приложение 2 са дадени интегралните граници на c2-разпределението c2(n,a), за които функциите на разпределение P имат определени стойности P =   1 - a. В приложението тези стойности на P са 0.01, 0.05, 0.10, 0.50, 0.90, 0.95 и 0.99 при степените свобода n от 1 до 20.  Числата  0.01, 0.05  и  т.н.  се наричат статистическа сигурност Р, защото със съответната вероятност (статистическа сигурност) може да се твърди, че случайната величина заема стойности в интервала, определен от нула и интегралните граници. Т.е. интеграл от плътността на c2-разпределението от нула до c2(n,a) е равен на P = 1 - a.

Тези получени като a =   1 - P се наричат статистическа значимост. На фигура 2 са показани интегралните граници за две c2-разпределения с различни степени на свобода.

.
Фигура 2. Интегрални граници на c2-разпределения със степени свобода, съответно 2 и 3 и статистическа сигурност P = 0.50. От приложение 2 се вижда, че те са съответно c2(2,0.50) = 1.39 и c2(3,0.50) = 2.27.

Пример 1.

а) Да се пресметне вероятността случайната величина  c25 да заема стойности по-малки от 4.3.

б) Да се намери интервалът (0, Х), в който случайната величина c29 заема стойности с вероятност 0.90.

Решение:

 а) От приложение 2 се вижда, че за степени свобода 5 от интегралните граници най-близка до 4.3 е 4.35. Следователно

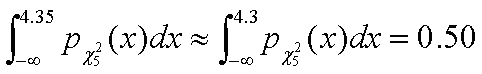
б) Търси се Х, за което

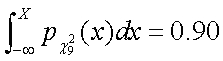
Фактически долната граница на горния интеграл е нула, понеже плътността на c2-разпределението е нула за Х < 0.

От същата таблица за степени свобода 9 и статистическа сигурност P = 0.90 се намира интегрална граница, c2(9,0.10)равна на 14.7. Интервалът е (0,14.7).

Пример 2. Да се намери вероятността отношението S2/s2 да е в интервала (0,1), където S е стандартното отклонение от десет измервания, а s2 е дисперсията на тяхното разпределение.

Решение: Условието 0 < S2/s2 < 1 e еквивалентно на 0 < 9 S2/s2 < 9, а величината 9S2/s2 е c29 разпределена (S е станадартното отклонение на десетте резултата), т.е. търси се вероятността случайната величина c29 да е в интервала (0,9). От приложение 2 за f = 9 се вижда, че 9 е между интегралните граници 8.34 (за Р = 0.50) и 14.7 (за Р = 0.90), но по-близко до първото число, т.е. търсената вероятност е около 0.50.

( съдържание )

Автор: Пламен Пенчев, Ph.D.

[ това е материал от брой 32 от август 2009 г. на списание "Коснос" www.kosnos.com ]