Колебание на двуатомна
молекула
.
(съдържание)
В настоящия материал ще разгледаме по-подробно колебанието (вибрацията) на двуатомна молекула като първо ще приведем системата от две уравнения на движение до едно уравнение. След това ще разгледаме вибрирането на отделните атоми и ще покажем, че те се движат с еднаква честота и еднаква фаза. Ще използваме класическото приближение за хармоничен осцилатор. Както беше изяснено в гореспоменатия материал то дава същата формула за честота на вибрация на молекулите както и квантовомеханичния модел. Също така, там може да намерите информация за физическия смисъл на величините и спектроскопското значение на този модел.
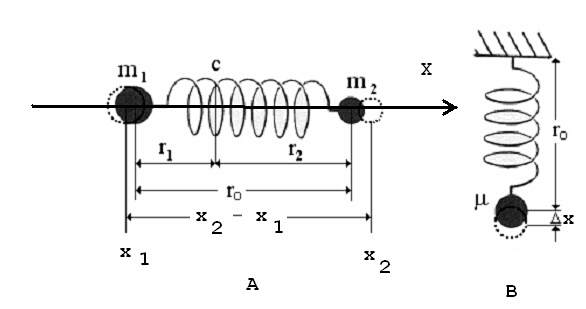
1. Честота на вибрация на двуатомна молекула. Избираме координатната система (фигура 1A) с ос X, ориентирана от m1 към m2. При разтягане на пружината (връзката) на всяка от масите m1 и m2 действа една и съща по величина сила, но с различен знак. Величината на силата зависи от изменението на равновесното разстояние между двете маси, последното от които е равно на r0. Очевидно, че разстоянието между масите винаги е x2 - x1, и затова изменението на равновесното разстояние се дава като x2 - x1 -r0.

При разтягане на пружината на първата маса действа сила надясно (пружината се стреми да се свие), т.е. при положително изменение на дължината между масите силата е положителна, а на втората, поради същата причина силата е наляво, т.е. при положително изменение на дължината между масите силата е отрицателна. Тогава двете уравнения за втория закон на Нютон за двете маси в хармонично приближение (силата зависи линейно от изменението на разстоянието) са следните:
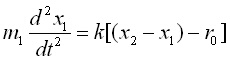
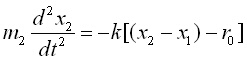
Ако разделим първото уравнение на m1, а второто на m2, и от новополученото второ извадим новополученото първо ще получим следното уравнение:
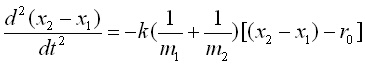 (2)
(2)
!
Във
физиката първа производна по времето се
записва с точка върху величината, а втора
- с две точки. По долу ще използваме традиционния
запис с "прим" и "секонд".
!
! Не забравяйте, че диференцирането
от коя да е степен е линеен оператор и затова
можем да запишем, че разлика от втори производни
по времето на две величини е равна на втората
производна по времето от разликата между
тях. Също така в производната може да вмъкваме
константа, защото коя да е производна от
нея е нула.
Съгласно двете забележки лявата част на (2) беше преобразувана и може да се допреобразува така:
x2" - x1" = (x2 - x1)" = (x2 - x1 - r0)" = Dx"
С Dx = (x2 - x1 - r0) означихме изменението на дължината на връзката. Както виждаме от (2) и новите преобразувания на лявата му част, Dx се среща в ляво и в дясно на израза. Допълнително, в дясната част намираме познатия израз за приведената маса m, 1/m = 1/m1 + 1/m2. С тези преобразувания от (2) получаваме изразът (3).
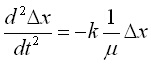 (3)
(3)
Това на практика е уравнение на трептене на една материална точка, закачена на една пружина, която има същите свойства като пружината между двата атома и има маса, равна на приведената маса на двата атома - вижте фигура 1B. Движението на тази маса се описва с една косинусоида (или синусоида, в зависимост от началната фаза j0), уравнение (4):
Dx = A cos(wt + j0) (4)
Величината A се нарича амплитуда, w - кръгова честата, а както споменахме по-горе j0 е начална фаза на трептенето. Кръговата честота е равна на
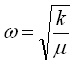 (5),
(5),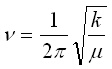 (6)
(6)
Написано уравнение (4) с честотата, а не кръговата честота изглежда по следния начин:
Dx = A cos(2pnt + j0) (4a)
Същият резултат е даден и в материала "Вибрационна спектроскопия", на който настоящия материал се явява един вид математическо допълнение.
2. Център на масите. От физиката е известно, че всяко едно движение на две тела може да бъде приведено математически в задача за движение на едно тяло с маса, равна на приведената маса на двете тела. Може да се докаже, че центърът на масите (тежестта) продължава да се движи праволинейно и без ускорение във външна отправна система, т.е. той не трепти.
При така избраната координатна система центърът на масите лежи на остта X и има координата
xc = (m1x1 + m2x2)/(m1 + m2) (7a)
! Координатите yc и zc са равни на нула, понеже и y и z координатите на двете точки са равни на нула.
Изразът (7a) можем да запишем като (7b):
m1x1 + m2x2 = (m1 + m2)xc (7b)
Ако с r означим разстоянието между двата атома, то очевидно имаме
x2 - x1 = r (8)
Ако умножим (8) с m1 и го съберем с израз (7b) получаваме
(m1 + m2)x2 = m1r + (m1 + m2)xc
което преобразуваме до
(m1 + m2)(x2 - xc) = m1r (9a)
или
(x2 - xc) = m1r/(m1 + m2) (9b)
Аналогично ако умножим (8) с m2 и и го извадим от израз (7b) получаваме
(m1 + m2)x1 = - m2r + (m1 + m2) xc
което преобразуваме до
(m1 + m2)(xc - x1) = m2r (10a)
или
(xc - x1) = m1r/(m1 + m2) (10b)
Разделянето на (9a) на (10a) или (9b) на (10b) дава
(x2 - xc)m2 = m1(xc - x1) (11a)
Ако вместо разстоянията в кой да е момент от време между атомите и центъра на масите и това между самите атоми, изберем съответните равновестни разстояния, то последните също ще задоволяват изразите (10a) и (10b) и (9a) и (9b) - за означенията вижте фигура 1A.
(m1 + m2)r2 = m1r0 (9c)
r2 = m1r0/(m1 + m2) (9d)
и за атом 1
(m1 + m2)r1 = m2r0 (10c)
r1 = m1r0/(m1 + m2) (10d)
Разделянето на (9c) на (10c) или (9d) на (10d) дава
m2r2 = m1r1 (11b)
3. Движение на отделните атоми. Изразът (4a) може да преобразуваме по следния начин (прехвърляме r0 отдясно):
x2 - x1 = r0 + A cos(2pwt + j0) (4b)
m1x1 + m2x2 = (m1 + m2)xc (7b)
ако умножим (4b) с m1 и го съберем със (7b) ще получим:
(m1 + m2)x2 = (m1 + m2)xc + m1[r0 + A cos(2pwt + j0)]
или
Аналогично, ако умножим (4b) с m2 и го извадим от (7b) ще получим:
(m1 + m2)x1 = (m1 + m2)xc - m2[r0 + A cos(2pwt + j0)]
или
Имайте предвид, че десните части на (12a) и (12b) не са удълженията на r1 и r2, които ще означим с Dx1 и Dx2 ! За да получим Dx2, което е преместване на втория атом при трептенето, трябва от (12a) да извадим (9d)
r2 = m1r0/(m1 + m2) (9d)
Получаваме
Dx2 = [(x2 - xc)- r2] = [m1/(m1 + m2)][Acos(2pwt + j0)] (13a)
Аналогично, ако от (12b) да извадим (10d)
r1 = m1r0/(m1 + m2) (10d)
Dx1 = [(xc - x1)- r1] = [m2/(m1 + m2)][Acos(2pwt + j0)] (13b)
Сравнението на (13a) и (13b) показва, че двата атома се движат с еднаква честота w и еднаква начална фаза j0. Това е много важен резултат, който за многоатомни молекули може да се обобщи, че при едно дадено нормално трептене атомите се движат с еднаква честота и еднаква фаза, като последното означава, че атомите достигат крайните си положения в един и същ момент от време.
Разбира се, амплитудите на отклоненията им не са равни, а в частен случай някои атоми не се движат при дадено нормално трептене на многоатомните молекули. В конкретния случай отношението на преместванията на атомите е обратно пропорционално на техните маси - вижте израз (14), който се получава при деление на (13a) на (13b).
Dx2 / Dx1 = m1 / m2 (14a)
m2 Dx2 = m1 Dx1 (14b)
На практика, отношенията (14) означава, че в общия случай амплитудите на трептенията не са равни (при неравни маси). Те са равни, само ако масите са равни. Ако не бяха изпълнени (14) щеше при трептенето да се премества центъра на тежестта, т.е. да има транслация.
Нека сега си представим, че едната маса е много по-голяма от другата, например m1 >> m2. В израза (13a) отношението в първите квадратни скоби става единица (просто се пренебрегва m2) и трептенето става
Dx2 = [(x2 - xc)- r2] = Acos(2pwt + j0) (15a)
докато в израза (13b) отношението в първите средните става близко до нула и целия израз става
Dx1 = [(xc - x1)- r1] = 0[Acos(2pwt + j0)] = 0 (15b)
т.е. атом 1 (който е по-тежък) не се движи, а само атом 2 (който е по-лек) трепти. Разбира се трептенето на втория атом е с различна амплитуда и различна честота (която зависи от приведената маса, като последната сега е равна на масата на втория атом). Единствено фазата не се променя.
Литература
1. Г. Андреев. Молекулна спектроскопия, Изд. ПУ “П. Хилендарски”, Пловдив, 1999.
2.
Автор: д-р Пламен Пенчев