Както беше казано във втората лекция, точковите групи на симетрия са определен вид групи в алгебрата. Групата в алгебрата е съставена от елементи, за които е дефинирана операцията "умножение", и която операция е асоциативна, а резултатът от това "умножение" е винаги елемент, който принадлежи на групата. Т.е. ако означим елементите на групата с a, b, c и d то имаме
a * b = c; c принадлежи на групата
и операцията "умножение" е асоциативна
(a * b) * c = a *( b * c) = d
Има още две други изисквания: (1) в групата да има елемент на групата, наречен "единичен елемент", който умножен с кой да е елемен да дава последния:
e * b = b и b * e = b
и (2) всеки елемент на групата да има обратен елемент, за който
b-1 * b = e и b * b-1 = e
където e е единичния елемент. Операцията "умножение" не е задължително да бъде комутативна, т.е. в общия случай не се изпълнява a * b = b * a.
В точковите групи на симетрия, които разгледахме досега (например, групата D3h на молекулата на борния хидрид, BH3), операциите на симетрия (а не елементите на симетрия) бяха елементи на точковите групи. Ролята на единичен елемент на групата изпълняваше операцията за идентичност, означавана с Е, а както видяхме от таблицата за умножение на операциите на симетрия в тази група, всяка операция има своя обратна операция, която изпълнена след нея довежда молекулата до оригиналната номерация на атомите (или операцията на симетрия, изпълнена след обратната операция не променя номерацията на атомите в молекулата).
Теоретически, може да има безкрайно (макар и изброимо) число точкови групи на симетрия, но в химията са важни само няколко, поради спецификата на строежа на химичните съединения, в които валентността не надминава 8. А това са групите, в които остта от най-голям порядък Cn има n < 7. Най-просто устроената група е C1, в която има само една операция на симетрия - операцията за идентичност, Е. Това е групата на несиметричните (асиметричните) съединения, като молекулата на CHFClBr (флуоро хлоро бромо метана). Следват две групи, CS и Ci. CS има следните елементи: Е и sh, а CS - Е и i. Молекулата на хлорформалдехида има равнинна симетрия, CS, а молекулата на мезо-винената киселина - симетрия Ci.
Останалите групи, които представляват интерес за химията са:
C2, C3, C4, C5, C6, D2, D3, D4, D5, D6,
C2v, C3v, C4v, C5v, C6v, C2h, C3h, C4h, C5h, C6h,
D2h, D3h, D4h, D5h, D6h, D2d, D3d, D4d, D5d, D6d,
S4, S6, T, Td, Th, O, Oh, I и Ih
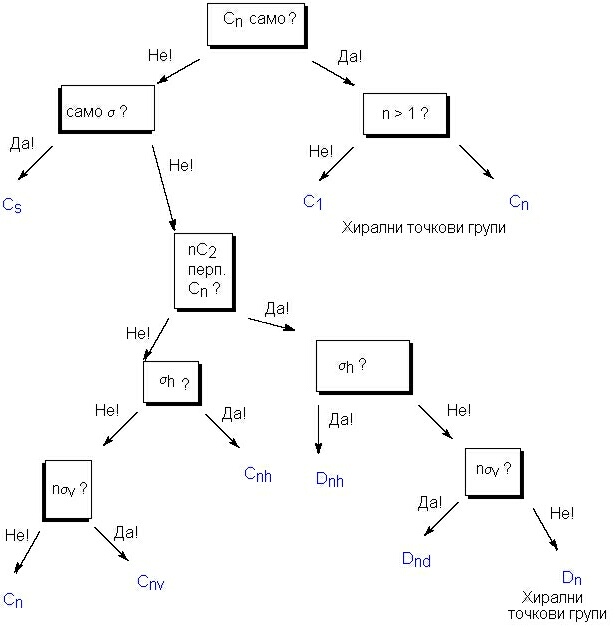
В повечето учебници се дават логически схеми за определянето на групата на симетрия. Ето една от тях. В правоъгълниците се проверява наличието на даден елемент на симетрия. Обърнете внимание, че "nC2 перп. Cn?" означава "Има ли n на брой оси от втори порядък, които са перпендикулярни към остта от най-висок порядък?"
