В тази лекция ще стартираме спецификацията на един клас, който представя комплексните числа. Засега целта ни е да покажем колко богат и многостранен програмен език е C⁺⁺,  и как може да създаваме свои собствени типове от данни. В бъдеще ще доразвием този клас и с него ще въвеждаме останалите концепции на обектно-ориентираното програмиране. Трябва да отбележим, че това ще бъдат само програми с учебна цел, защото самият програмен език C⁺⁺ има клас complex, който представлява шаблон (template class). Този шаблон представя, и манипулира с, комплексни числа. Но нека първо си припомним какво представляваха комплексните числа.

1. Комплексни числа. Те са сума от две числа - реално и имагинерно число. До представата за имагинерни числа се стига при коренуване на отрицателни числа. Така например корен квадратен от -1 (минус единица) се записва с числото i. Т.е. аритметичните операции, които са дефинирани за реалните числа нямат резултат само реални числа и резултатът от тях излиза извън областта на реалните числа: имагинерно = операция(реално). По същия начин, прилагането на аритметичните операции върху имагинерни числа води до реални. И за да няма противоречии се въвеждат т.н. комплексни числа, които представляват наредена двойка от реално число и комплексно число - z = (a, b). Числото a  се нарича реална част на z, а числото b - имагинерна част на z, като те се отбелязват съкратено с x = Re(z) и  y = Im(z).

Две комплексни числа, (a₁, b₁) и (a₂, b₂), се събират или изваждат като се събират или изваждат съответните им части:

Всяко комплексно число z има спрегнато число на него, което се отбелязва с чертичка над него `z или със звезда след него z*. То има същата реална част, но неговата имагинерна част е обратна по знак:

Вместо като наредени двойки, комплексните числа могат да се записват и като сума, в която имагинерната част се преставя във вид на произведение на имагинерното число i (корен от минус единица) и имагинерната част. Например (a, b)= a + ib. Този запис позволява по-лесно извършване на аритметичните действия с комплексните числа: например за събирането получаваме:

По същия начин може да се получи и произведението на две комплексни числа, само трябва да се има предвид че i² = -1 .

където с x сме отбелязали знака за умножение.

От тази формула се вижда, че произведението на едно комплексно число по неговото спрегнато дава реално число, което е равно на сума от квадратите на частите на комплексното число.

Корен квадратен от това произведение се нарича модул на комплексното число и се бележи с |z| или Mod(z). Тази величина още се нарича големина на комплексното число или негова абсолютна стойност.

Като използваме горната формула и като умножим числителя и знаменателя с комплексно спрегнатото на делителя, за частното на две комплексни числа получаваме:

Останалите действия с комплексните числа, както и тяхното експоненциално представяне (формула на Ойлер) ще бъдат разгледани в специална лекция в списанието ни.

2. Потребителски клас Complex_number. Ако нямаше клас в C⁺⁺, който борави с комплексните числа, защо бихме искали да създадем такъв клас. Първо, ще можем лесно да дефинираме променливи от новия клас, например Complex_number z1, z2;. Второ, ще можем да използваме редица оператори, които са дефинирани само за предефинираните типове. Например, ще можем да записваме в нашия код

z3 = z1 + z2;
z3 = z1 - z2;
z3 = z1 * z2;
z3 = z1 / z2;

По същия начин много нови типове данни могат да бъдат създавани и програмистът ще може да борави с тях, така както и с предефинираните типове. Например на програмиста може да му се наложи да работи със следните типове данни [1]:

 - времето на деня, с часовете, минутите и секундите като отделни числа;
 - дати, които включват в себе си годината, месеца и деня;
 - прости и сложни дроби с челочислена част, числител и знаменател;
 - точки или вектори в равнината - (x ,y)  или пространството - (x ,y, z);

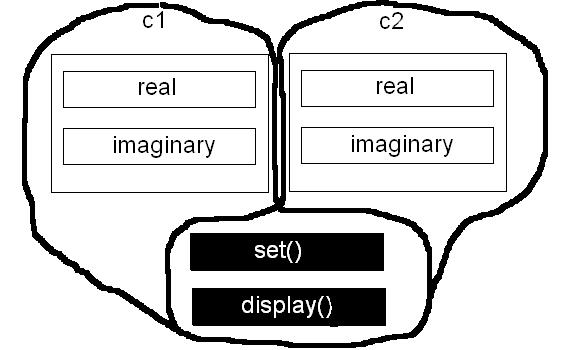
3. Примерна програма с класа Complex_number. По-долу е дадена програмата. В класа има две променливи (instance data) за двете части на комплексното число - real и imaginary. Функцията set() запитва потребителя за двете части на класа, а функцията display()  представя комплексните числа на екрана.

// complex1.cpp
// a class that models a complex number  data type

#include <iostream.h>
#include <conio.h>       //for getche()

class Complex_number
{
  private:
    float real;          // real part
    float imaginary;     // imaginary part
  public:
    void set()
    {
      char dummy;        // for comma

      cout << "Enter number (format Re, Im): ";
      cin >> real >> dummy >> imaginary;
    }

    void display()
    {
      cout << '('
           << real       // real part
           << ','
           << imaginary  // imaginary part
           << ')';
    }
};  // class Complex_number

void main()
{
  Complex_number c1, c2; // create two complex_number variables

  cout << "For c1, ";
  c1.set();       // set c1
  cout << "For c2, ";
  c2.set();       // set c2

  cout << "\nc1 = ";
  c1.display();   // display c1
  cout << "\nc2 = ";
  c2.display();   // display c2

  c2 = c1;        // make c2 equal to c1
  cout << endl << "\nc1 = ";
  c1.display();   // display c1
  cout << "\nc2 = ";
  c2.display();   // display c2

  // stop the flow on the monitor
  getch();
}  //end main

Обърнете внимание, че стойността на един обект може да се присвоява на друг с помощта на оператора за присвояване, точно така както е за предефинираните типове. В програмата това е твърдението c2 = c1;. Фактически двете променливи real и imaginary на обекта c2 стават равни по стойност с тези на c1. Всъщност, в C⁺⁺ всяка една променлива е обект, независимо дали е от потребителски дефиниран тип или предефиниран тип.

4. Обектите в паметта на компютъра. Видяхме как става присвояването на един обект на друг. На практика, за всеки един обект от даден клас в паметта се отделя отделно място за неговите променливи. Затова при присвояване между обектите, стойностите от едните места в паметта се копират на другите места в паметта. Но не е така с функциите на класа. В паметта се пази само едно копие на всяка една от функциите на класа. Тези концепции, илюстриращи се с двата обекта в горната програма c1 и c2, са представени на следната фигура.

От това представяне в паметта има изключения, например ако някоя променлива в класа е дефинирана с ключовата дума static,  то за всички обекти в програмата тази променлива е една и съща и заема само едно място в паметта.

[1] Robert Lafore; C++ Interactive Course. Waite Group Press, Macmillan Computer Publishing, 1996.

Автор: Проф. Процесор Аритметиков

Keywords: С++,  OOP programming , C++ , Classes , Inheritance , Reusability , Creating New Data Types , Polymorphism and Overloading
Ключови думи: клас , обект, обектно ориентирано програмиране , полиморфизъм switch if else ?