Статистически оценки на параметрите на разпределението

( съдържание )

С този материал започнахме една поредица за приложение на статистиката в химията. Материалът може да се използва не само от химици, а от всички, които се занимават с обработка на експериментални резултати. В тази лекция ще разгледаме някои статистически оценки на параметрите на разпределение.

Получените при измерванията случайни величини са независими една от друга и същевременно разпределени нормално с едни и същи параметри m и s2. Ето защо те представляват един вид "реализации" на една, в повечето случаи нормално разпределена случайна величина. Разбира се, измерванията могат да бъдат и с друго разпределение, но опитът сочи, че в химията повечето измервани величини имат нормално разпределение, затова в този материал всички изводи ще се основават на предпоставката, че измерванията са независими случайни величини, разпределени с едни и същи параметир (математическо очакване и дисперсия) и са нормално разпределени.

Всеки набор от експериментални стойности се нарича извадка от генералната съвкупност. Под генерална съвкупност се разбира извадка с неограничен обем, т.е. такава извадка, която напълно характеризира случайната величина. Като понятие генералната съвкупност напълно се припокрива с понятието разпределение, но боравенето с такъв безкраен набор от реализации на случайната величина е по-близко до сетивните представи на човека, отколкото кривата на разпределение. Много често се казва "генерална съвкупност с едикакво си разпределение", което не противоречи на изложеното тълкуване. Както беше обяснено в първия параграф, понятието величина се асоциира с понятието стойност и най-естественото съпоставяне (досега непротиворечащо на човешката практика) е за стойност на величината да се приема математическото очакване на разпределението на получаваните случайни величини. Затова една от задачите на експериментатора е получаване на оценка на математическото очакване с помощта на извадката случайни величини. Числената стойност на дисперсията определя вероятността за появата на дадена случайна величина в определен интервал и тъй като всяка една оценка е случайна величина, то за да се определи интервалът, в който е най-вероятно да се намира математическото очакване, е необходимо да се оцени и дисперсията. Оценки на М(Х) и D(Х) са средната стойност и стандартното отклонение.

1. Средна стойност. Тя се дефинира за N стойности по уравнението

`Х = (Х1 + Х2 + ... + ХN)/N =  SХk/N     (1)

Средната стойност е случайна величина, която също е разпределена нормално със собствени   и о. Математическото и очакване (прилагайки свойства на математическото очакване, вижте този материал) е равно:

M(`Х ) = М(SХk/N) = (1/N)SM(Хk) = (1/N)SM(Х) = (1/N)NМ(Х) = (1/N)M(Х)

т.е. математическото очакване на средната величина на N случайни стойности съвпада с математическото им очакване. Такава статистическа оценка, за която математическото и очакване съвпада с оценяваната величина, се нарича неизместена оценка. Аналогично се доказва, че дисперсията на разпределението на средните стойности е 1/N от дисперсията на случайните величини.

D(`Х ) = D(SХk/N) = (1/N)2SD(Хk) = (1/N)2SD(Х) = (1/N)2ND(Х) = (1/N)D(Х)

Тук под внимание бе взето, че отделните измервания са независими случайни величини.

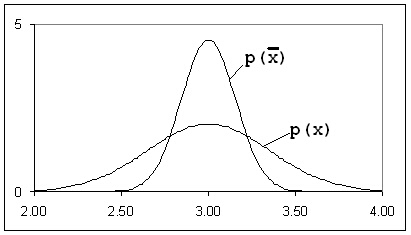
На практика това означава, че са проведени няколко серии от измервания на една величина и са определени техните средни стойности. Разпределението на средните стойности и това на случайната величина имат еднакви математически очаквания. Но дисперсията на`Х е  s2/N, т.е. разсейването на средните стойности около стойността на величината са по-малки, и по-добре я приближават от коя да е измерена стойност. Това нагледно е представено на фигура 1..

Фигура 1. Разпределения: (1) на нормална случайна величина; (2) на средната стойност от N нейни реализации; N = 5.

Ако някои от измерванията се повтарят, формула (1.6) може да се обобщи

`Х = (n1Х1 + n2Х2 + ... + nNХN)/N =  SnkХk/N =  S(nk/N)Хk   (2),

където nk е броят резултати със стойност Хk; S(nk = N.

Числата (nk/N) са честотите на поява на стойностите Хk и при нарастване на N клонят към вероятностите pk за появата на Xk, т.е. при голямо N се изпълнява равенството (вижте формула (1.1) от този материал):

`Х = S(nk/N)Хk  = SpkХk  = M(X)  (3)

Следователно средната стойност клони във вероятностен смисъл към математическото очакване. Такава оценка, която при нарастване обема на извадката клони по вероятност към оценяваната стойност, се нарича състоятелна оценка. Практически това означава, че при нарастване на големината на една извадка, нейната средна стойност се доближава до стойността на измерваната величина.

2. Стандартно отклонение. За N стойности стандартното отклонение се нарича величината S, чийто квадрат е равен на

S2 = [(Х1 -`Х)2 + ... + (ХN -`Х)]/(N-1) = [S(Хk -`Х)2]/(N-1)   (4)

Стандартното отклонение също е случайна величина, като  величината

c2 = S2(N-1)/s2

е c2 разпределена (за хи-разпределението ще научите в следващия материал). S2 е неизместена оценка на дисперсията. Логичен е въпросът защо в знаменателя на (4) не стои N. Изразът

S((Хk -`Х)2/N   (5)

е изместена оценка на дисперсията, но и S2  и (5)са състоятелни оценки на дисперсията - просто при нарастване на N се заличава разликата между N и N-1.

Задача 1. Докажете, че изразът (5) е изместена оценка на дисперсията, а S2 е неизместена оценка.

Вижте решението на задачата. (решението на задачата ще бъде дадено в брой 29 от април 2009 г.)

Пример 1. В таблица 1. са дадени десет серии от по десет измервания на желязо в питейна вода. Да се намерят средните стойности и стандартните отклонения.

Таблица 1. Десет серии от анализи на желязо в питейна вода.

No на серия    Съдържание на желязо в питейна вода (в mg/ml)

1          6.23 6.29 6.17 6.17 6.15 6.29 6.31 6.02 6.33 6.24
2          6.20 6.14 6.17 6.09 6.09 6.22 6.26 6.09 6.15 6.32
3          6.28 6.36 6.24 6.40 6.27 6.19 6.36 6.24 6.12 6.16
4          6.21 6.34 6.20 6.16 6.21 6.20 6.10 6.36 6.21 6.32
5          6.25 6.24 6.23 6.30 6.46 6.36 6.31 6.31 6.34 6.24
6          6.07 6.39 6.24 6.19 6.23 6.23 6.24 6.29 6.30 6.15
7          6.05 6.43 6.24 6.25 6.25 6.34 6.26 6.33 6.44 6.17
8          6.26 6.33 6.35 6.28 6.18 6.14 6.13 6.30 6.27 6.15
9          6.25 6.25 6.40 6.32 6.20 6.29 6.30 6.37 6.36 6.13
10         6.30 6.17 6.30 6.27 6.03 6.39 6.22 6.11 6.19 6.15

Решение: Когато се изчислява на ръка или с калкулатор е целесъобразно да се смята само със стойностите, които се променят от резултат на резултат (в случая само с десетите и стотните, а шестицата не се взима под внимание). Като се приложи (1), се получава за първата серия:

`Х = (23+29+17+17+15+29+31+2+33+24)/10 = 22  /в стотни/,

т.е.`Х = 6.22.

Аналогично по (4) се получава:

S2 = [(23-22)2+(29-22)2+(17-22)2+(17-22)2+(15-22)2+
+(29-22)2+(31-22)2+(2-22)2+(33-22)2+(24-22)2]/9 =
 = 81

или S2 = 81 / в стотни /, т.е. S = 0.09.

За десетте серии се получават следните резултати:

No на серия   1     2    3    4     5     6     7     8     9     10

`Х            6.22  6.17 6.26 6.23  6.30  6.23  6.28  6.24  6.29  6.21
 S            0.09  0.08 0.09 0.08  0.07  0.09  0.12  0.08  0.08  0.11

Една по-точна оценка за резултата (математическото очакване) е средното на десетте средни стойности, а за дисперсията средното на квадратите на десетте стандартни отклонения (само при равен брой на измерванията във всички серии, вижте следващите материали). Съответно се получава`Х = 6.25 и S = 0.099 = 0.1

( съдържание )

Автор: Пламен Пенчев, Ph.D.

[ това е материал от брой 28 от март 2009 г. на списание "Коснос" www.kosnos.com ]