Точно както има обекти с масиви в тях, така може да има и масиви от обекти. Това е много удобна конструкция, която позволява серийно обработване на обектите в програмата.

1. Дефиниране на масив от обекти. Дефинирането на масив от обекти става така както се дефинира масив от всеки един друг тип. Например масив от 20 комплексни числа се дефинира по следния начин:

complex_number cn[20];

Разбира се, класът complex_number трябва да е специфициран преди горната дефиниция. Спецификацията на класа complex_number бе дадена в част 11 на този курс и включваше две променливи на класа - real и imaginary. А в част 14 на този курс бяха дефинирани функциите, които извършват четирите аритметични операции с комплексни числа. В настоящата лекция ние ще разширим тази спецификация като включим абсолютната стойност на комплексното число - abs и аргумента му - arg. В кода по-долу за краткост не са дадени функциите за изваждане и делене на комплексно число, но е добавена една нова функция, която намира m-тия подред n-ти корен от комплексното число (едно комплексно число има n на брой  n-ти корени).

class complex_number
{
  private:
    float real;       // real part
    float imaginary;  // imaginery part
    float abs;        // absolute value
    float arg;        // argument
  public:
    void set()
    {
      char dummy;        // for comma
      float a, b;

      cout << "Press i for Re + Im*j or press e for Abs*e^Arg: ";
      dummy = getche();
      if (dummy == 'i')
      {
        cout << "\nEnter Re: ";
        cin >> real;

        cout << "Enter Im: ";
        cin >> imaginary;

        abs = sqrt(real*real + imaginary*imaginary);
        if (real != 0)
          if (real > 0)
            arg = atan(imaginary/real);
          else
            arg = atan(imaginary/real) + M_PI;
        else
          if (real > 0)
            arg = M_PI/2;
          else
            arg = -M_PI/2;
      }
      else
      {
        cout << "\nEnter Abs: ";
        cin >> abs;

        cout << "Enter Arg: ";
        cin >> arg;

        real = abs*cos(arg);
        imaginary = abs*sin(arg);
      }
    }  // void set()

    void display()
    {
      cout << '('
           << real       // real part
           << " , "
           << imaginary  // imaginary part
           << ')';
      cout << " ["
           << abs       // real part
           << " * e( i*"
           << arg  // imaginary part
           << " ) ]";
    }

    void add(complex_number compl_num)
    {
      real += compl_num.real;
      imaginary += compl_num.imaginary;
    }

    void mult(complex_number compl_num)
    {
      complex_number cn;
      cn.real = real;
      cn.imaginary = imaginary;

      real = cn.real*compl_num.real - compl_num.imaginary*cn.imaginary;
      imaginary = cn.real*compl_num.imaginary + compl_num.real*cn.imaginary;
    }

    complex_number root_compl_num(int m, int n)
    {
      float phase = arg / n;
      complex_number root;

      root.abs = exp(log(abs)/n);
      root.arg = phase + m*2*M_PI/n;
      root.real = root.abs*cos(root.arg);
      root.imaginary = root.abs*sin(root.arg);

      return root;
    }
};  // class complex_number

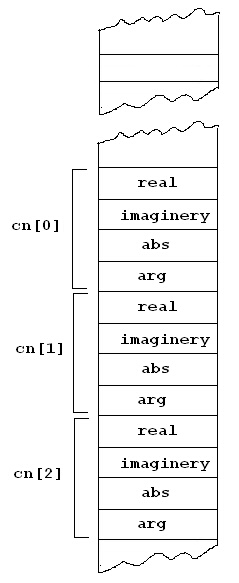
Всички променливи на обектите от масива се съхраняват последователно в паметта по следния начин (на картинката паметта схематично се запълва отгоре надолу):

В класа има три функции, които са ни познати от предишните лекции - set(), display() и add(complex_number compl_num). Те са дефинирани в публичната област на класа. Функцията set()е изменена така, че потребителят може да вкарва комплексното число с неговите реална и имагинерна част или с неговата абсолютна стойност и аргумент. Съответно функцията display() е изменена, така че показва и двата записа на комплексното число едновременно - Re + iIm и |z|е^iq.

Когато имахме дефинирани два обекта c1 и c2, обръщането към, например, третата функцията ставаше по следния начин

c1.add(c2);

При дефиниран масив от обекти обръщането към тези функции няма да става само с името на масива (както грешно е дадено по-долу)

cn.add(c2);   // error!!!

а с помощта на индексна променлива, която се дава, заградена от индексния оператор [ ] (subscript operator [ ]):

cn[13].add(c2);

С това извикване добавяме комплексното число c2 към 14-тия елемент на масива cn[13].

2. Корен n-ти от комплексно число. В част 10 се запознахме с комплексните числа и операциите събиране, изваждане, умножение и делене. Сега ще се запознаем с коренуването на комплексните числа.

! Допълнителни знания за комплексните числа може да получите от материала "Комплексни числа" от брой 43 на списанието.

За всяко едно комплексно число z има n на брой комплексни числа w_k; k = 0, 1, ... n-1, които удовлетворяват равенството w_kⁿ = z. Т.е. всяко едно комплексно число има n на брой n-ти корени. Ако комплексното число z се представи в експоненциална форма z = |z|е^iq, където |z| е абсолютната стойност на z, а q - неговият аргумент, то k-ият n-ти корен се намира по следния начин w_k = |w|е^{i(q + k2p)/n}, за k = 0, 1, ... n-1, където реалното число |w| е n-ти корен от реалното число |z|, т.е. |w|ⁿ = |z|.

Програмата complex3.cpp извършва намирането на корените на едно комплексно число и работи с n, което не надминава 20.

Една особеност е използването на константата p (числото пи, 3.1415926...). В заглавния файл (Header File) math.h има дефинирани няколко константи, свързани с числото p. Те са дадени по-долу.

---------      ------------------------------------
Name           Meaning
---------      ------------------------------------
M_PI           pi
M_PI_2         One-half pi
M_PI_4         One-fourth pi
M_1_PI         One divided by pi
M_2_PI         Two divided by pi
M_1_SQRTPI     One divided by the square root of pi
M_2_SQRTPI     Two divided by the square root of pi

Ето изходът на екрана от намирането на 4-те квадратични корена на реалното число -16, т.е. комплексното число (-16, 0).

For c1, Press i for Re + Im*j or press e for Abs*e^Arg: i
Enter Re: -16
Enter Im: 0

c1 = (-16 , 0) [16 * e( i*3.14159 ) ]
Enter root (n <= 20):4

=== The 4th roots are ===

root[1] = (1.41421 , 1.41421) [2 * e( i*0.785398 ) ]
root[2] = (-1.41421 , 1.41421) [2 * e( i*2.35619 ) ]
root[3] = (-1.41421 , -1.41421) [2 * e( i*3.92699 ) ]
root[4] = (1.41421 , -1.41421) [2 * e( i*5.49779 ) ]

А ето и изходът от същата операция, но същото число е вкарано в експоненциален вид: 16е^ip:

For c1, Press i for Re + Im*j or press e for Abs*e^Arg: e
Enter Abs: 16
Enter Arg: 3.1415926

c1 = (-16 , 2.41593e-06) [16 * e( i*3.14159 ) ]
Enter root (n < 11):4

=== The 4th roots are ===

root[1] = (1.41421 , 1.41421) [2 * e( i*0.785398 ) ]
root[2] = (-1.41421 , 1.41421) [2 * e( i*2.35619 ) ]
root[3] = (-1.41421 , -1.41421) [2 * e( i*3.92699 ) ]
root[4] = (1.41421 , -1.41421) [2 * e( i*5.49779 ) ]

Фактически, четирите корена се намират по върховете на един квадрат, чийто върхове лежат на окръжност с радиус 2 (2⁴ = 16), както е дадено на фигурата по-долу.

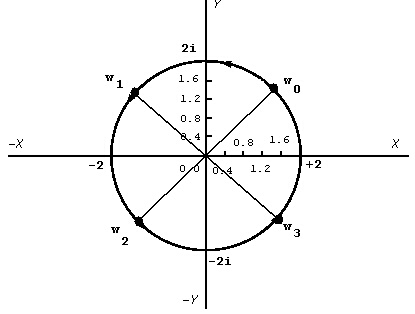
За упражнение, с програмата намерете корен четвърти от +16. Трябва да получите следните корени: 2, 2i, -2, -2i, които в експоненциална форма са: 2еⁱ⁰, 2е^ip/2, -2е^ip, -2е^i3p/2. Отново тези корени лежат на върховете на един квадрат, но той, сравнен с предишния, е извъртян по часовниковата стрелка на p/4, което е разликата на аргументите на двете комплексни числа, +16 и -16, делена на степента на корена, 4.

3. Други примери за масиви от обекти. В курса по програмиране на C++ на Лафоор [1]  са дадени два други примера - arrayair.cpp и arrayemp.cpp. Важно твърдение в първата програма е

at[n++].set();

което първо увеличава индексната променлива с единица, а после наглася обекта, който е елемент на масива. Другите оператори и дефиниции в тези две програми са лесно разбираеми и няма да Ви създадат проблеми.

С това свършваме лекциите за масивите. Масивът е полезна структура, но за съжаление размерът му се определя във времето за компилация, когато се дефинира масива. Ето защо потребителят трябва да осигури максималната стойност на броя на елементите на масива и много често от така заделената памет се използва само една малка част от нея, т.е. работи се с брой елементи много по-малък от максимално допустимия. Свързаните списъци или масиви от указатели могат да намалят количеството на използваната памет, както ще видим в по-следващите лекции на този курс.

Keywords: С++,  OOP programming , C++ , Classes , Inheritance , Reusability , Creating New Data Types , Polymorphism and Overloading
Ключови думи: клас , обект, обектно ориентирано програмиране , полиморфизъм switch if else ?