 (1)
(1)
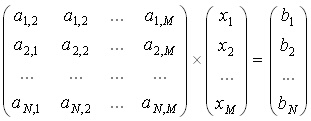
1. Решаване на системи от линейни уравнения. Много често в науката се търсят стойностите на няколко величини, които задоволяват едновременно няколко уравнения. Обикновенно броят на уравненията отговаря на броя на величините, чиято стойност се търси, но много по-често в науката броят на уравненията е по-голям от броя на неизвестните. В този случай се търсят стойностите на няколко величини, които най-добре удовлетворяват уравненията. Ако уравненията са линейни то задачата се записва по следния начин:
 (1)
(1)
където an,m са коефициентите на линейната система от уравнения, bn са свободните членове, а xm са неизвестните. В случая имаме система от N уравнения (n = 1, 2, ...N) с M неизвестни (m = 1, 2, ...M).
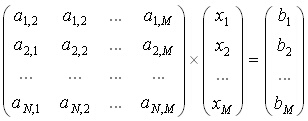
Уравнение (1) на практика е едно матрично уравнение, AX = B, което се изразява чрез N уравнения:
 (2)
(2)
Системата има само едно решение, ако рангът на матрицата A е равен на ранга на матрицата {AB} и те са равни на M, което е броят на неизвестните: Под матрицата {AB} разбираме матрица, в която първите M колони съвпадат с матрицата A, а последната колона е матрицата B. Записано математически това е rank(A) = rank({AB}) = M. Частен случай на предносказаното е, че ако N = M, то системата може да има точно едно решение и то при условие, че рангът на матрицата A е равен на M.
Когато N > M и рангът на матрицата A е равен на M, но рангът на матрицата {AB} е по-голям от M, системата се нарича преопределена и съществува едно решение, което заместено в уравненията дава изчислени свободни членове bn, които най-малко се отличават от bn. Решението е дадено с уравнение (3), което е изведено с матрици, чрез използване на обобщената обратна матрица на A, която е (ATA)-1AT, но същите зависимости могат да се изведат по метода на най-малките квадрати и така да се покаже, че решението (3) води до минимума на следната сума:
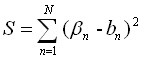
2. Многопроменлива линейна регресия [1-2]. На практика в науката се поставят задачи от вида на матричното уравнение (2), с които се цели да се изчислят величите bn, чрез стойностите на други величи xm. Такова едно изчисление реализира т.н. адитивна схема, а коефициентите xm се наричат инкременти. Реално линейните уравнения в (1) и (2) описват някакъв линеен модел и този модел е необходимо да описва възможно най-голям брой експериментални данни с малко на брой параметри, за да има този модел не само обяснителна, но предсказателна ценност. Това означава, че на практика N > M, и че системата няма решение, в смисъл, че няма такава комбинация от M параметъра, които да описват с произволна точност тези N уравнения. Но е напълно възможно системата да има решение, което да удовлетворява приблизително N-те уравнения, като по този начин това решение представлява необходимите параметри в линейния модел, които обясняват възможно най-голям брой експериментални данни.
Решението на матричното уравнение (1), AX = B, за правоъгълна матрица A може да се получи ако уравнението се умножи отляво с израза (ATA)-1AT
(ATA)-1ATAX = (ATA)-1ATB,
В лявата страна имаме умножение на матрицата (ATA) с нейната обратна (ATA)-1, което дава единичната матрица I и води до
IX = (ATA)-1ATB,
т.е.
X = (ATA)-1ATB (3)
Така получения набор от параметри – матрицата-колона X (т.е. наборът от неизвестните xm) параметризира линейният модел, с който се описва съответното природно явление.
Матрицата (ATA)-1AT се нарича обобщена обратна матрица на A и ако последната е квадратна очевидно имаме
(ATA)-1AT = A-1(AT)-1AT = A-1
3. Изчисляване на топлините на образуване на алкани с помощта на адитивна схема [3]. В лекцията "Топлина на образуване" видяхме, че стандартната топлина на образуване на линейните алкани, DHfo, може да се изчисли чрез броя на метиловите групи (които са само две) и броя на метиленовите групи, означени съответно с n(CH3) и n(CH2).
DHfo(CnCH2n+2) = -4.96 x n(CH2) - 10.06 x n(CH3)
или чрез броя на C-H и C-C връзките, означени по-долу съответно с n(C-H) и n(C-H) .
DHfo(CnCH2n+2) = hC-H x n(C-H) + hC-C x n(C-C)
което уравнение на практика е
DHfo(CnCH2n+2) = (2n+2) x hC-H + (n-1) x hC-C
защото в един алкан CnCH2n+2 има (2n+2)C-H и (n-1)C-C връзки.
В първата зависимост -4.96 и -10.06 са съответно инкрементите по метиленовите и метиловите групи, h(CH2) и h(CH3). Тази зависимост може да се обобщи за всички алкани, не само линейните, ако в нея добавим и инкременти за метиновите групи (CH) и четвъртичния въглероден атом (>C<).
DHfo(CnCH2n+2) = h(CH3) x n(CH3) + h(CH2) x n(CH2) + h(CH) x n(CH) + h(>C<) x n(>C<) (4)
За да използваме уравнение (4) е необходимо намирането на инкрементите h(CH3), h(CH2), h(CH) и h(>C<). Това се извършва с многопроменлив регресионен анализ на зависимостта на топлината на образуване от броя на метиловите, метиленовите и метинови групи и четвъртичните въглеродни атоми.
Втората зависимост по-горе (тази, която използва броя връзки в алканите) не може да различава между отделните изомери на даден алкан, тъй като те имат един и същ брой C-C и C-H връзки и затова не е подходяща за изчисляване на топлината на образуване на алканите. Този факт ще бъде изяснен в следващия пример, който използва данните от таблица 1.
Разбира се, че и схемата с използване на инкременти по метиловите, метиленовите и метиновите групи и четвъртичните въглеродни атоми също показва еднакви резултати при някои от изомерите на висшите алкани - например съединенията 2-метилпентан и 3-метилпентан имат един и същ брой такива фрагменти, но като цяло тя дава различна топлина на образуване за повечето изомери.
3.1. Изчисляване на топлините на образуване на алканите чрез решаване на система от N уравнения с N неизвестни.
Най-първо ще решим два примера, в които броят на инкрементите (в случая неизвестните) е равен на броя на уравненията, от които те се определят. След това ще разгледаме намирането на инкрементите при използване на уравнение (3).
Таблица 1. Брой на C-C
и C-H
връзки и стандартните топлини на образуване в газова фаза на шест алкана
[4].
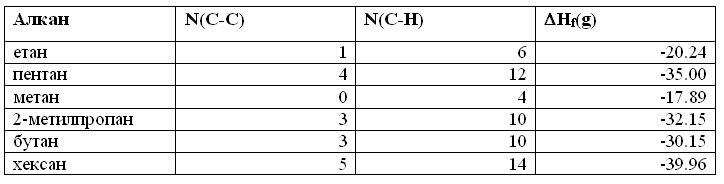
В четвърта колона на таблица 1 са дадени
топлините на образуване на шест алкана. Това са стандартните топлини на
образуване DHfo
за газовата фаза, при температура 298.15
K (25 oC) и 1
atm налягане, изразени в Kcall/mole.
Във втора и трета колона са дадени съответно броят на връзките C-C
и C-H
в тези съединения. Ако hC-C
и hC-H
са търсените инкременти (добавки) съответно за връзките C-C
и C-H,
то за намиране на една адитивна схема за изчисляване на топлините на алкани,
от данните за първите две съединения може да се състави системата от две
уравнения с две неизвестни:
| 1 x hC-C +
6 x hC-H = 20.24
4 x hC-C + 12 x hC-H = -35.00 |
(5) |
Ако първото уравнение се умножи с -2 и се прибави към второто, то за hC-C получаваме
2 x hC-C = (-2) x 20.24 + -35.00 = 5.48, което дава hC-C = -2.74. Ако заместим тази стойност на hC-C в кое да е от двете уравнения на (5) ще получим hC-H = -3.83. Обърнете внимание, че тези стойности на инкрементите са в Kcall/mole, тъй като стандартните топлини на образуване са в тези мерни единици и инкрементите имат същата размерност. С тези стойности в работната таблица "Alkanes - 2 vars" на Excel файла "heats_form.xls" са изчислени топлините на образуване на шестте алкана - клетки F2:F7. Както и се очаква, за двете използвани съединения, етан и пентан, имаме точно предсказване на топлините им на образуване, тъй като точно за тях беше решена система от две уравнения с две неизвестни, която има точно решение. Най-големи разлики (клетки G2:G7) от експерименталните имаме за метан и 2-метилпропан. Първото съединение няма C-C връзки, а второто е изомер на бутана и се описва със същия брой C-C и C-H връзки като него: 3 и 10. Това последното прави тази схема неприложима за различните изомери на алканите, които очевидно ще имат една и съща изчислена топлина на образуване, факт който не съвпада с реалността.
Тази система от две уравнения с две неизвестни може да бъде решена и с намиране на обратна матрица. Това е направено в същата работна таблица "Alkanes - 2 vars" на Excel файла "heats_form.xls". Ако представим броят на C-C и C-H връзките за етан и пентан като 2 на 2 матрица A в региона B2:C3, а неизвестните инкременти като 2 на 1 матрица X, и топлините на образуване като 2 на 1 матрица B в региона D2:D3, то е изпълнено
AX = B,
Ако умножим отляво двете страни с A-1 ще получим
X = IX = A-1AX = A-1B (6)
В гореспоменатия файл обратната матрица е намерена в региона B15:C16, а умножението A-1B е изпълнено в региона B18:B19.
Ако използваме три съединения - етан, пентан и 2-метилбутан и три инкремента - h(CH3), h(CH2) и h(CH), то тогава трябва да решим система от поне три уравнения с три неизвестни и това е направено по формула (6) в работна таблица "Alkanes - 3 vars" на Excel файла "heats_form.xls". Съответно матрицата A е с три реда и три колони и се разполага в региона B2:D4, матриците X и B са с три реда и една колона (матрица-колона) и последната е разположена в региона E2:E4, а матрицата X е изчислена в региона B18:B20.
3.2. Изчисляване на топлините на образуване на алканите чрез решаване на система от M уравнения с N неизвестни, където M > N.
В работна таблица "Alkanes
- 3 vars 5 Eqs" на Excel
файла "heats_form.xls"
са използвани пет уравнения с три неизвестни и е работено по уравнение
(3). Матрицата A
е с пет реда и три колони и се разполага в региона B2:E6,
матрицата X
е с три реда и една колона, и B
е с пет реда и една колона (отново матрица-колона) и последната е разположена
в региона F2:F6,
а матрицата X
е изчислена в региона B30:B32.
В екселската работна таблица са извършени и различните изчисления, които
са необходими и тяхната позиция е показана в следната таблица:
| Изчисление | Регион |
| AT | B11:F13 |
| (ATA) | B16:D18 |
| (ATA)-1 | B21:D23 |
| (ATA)-1AT | B26:F28 |
| (ATA)-1ATB | B30:B32 |
Последното изчисление дава стойностите на четирите инкремента (матрицата X). В региона F2:F9 са изчислени топлините на образуване на осем алкана. Обърнете внимание, че за първите пет алкана изчислените топлини не съвпадат с експерименталните и това е така, защото вече имаме пет уравнения с три неизвестни и намерените неизвестни дават при заместването си топлини на образуване, които са максимално близки до използваните (експерименталните) за намирането на инкрементите.
Аналогично, в таблица "Alkanes - 4 vars 6 Eqs" на Excel файла "heats_form.xls" са използвани 6 уравнения с четири неизвестни. След това получените четири инкремента са приложени за предсказване на стандартните топлини на образуване на пет алкана. Обърнете внимание, колко добре използваният модел предсказва разликата в топлините на образуване на двойките изомери 2-метилпропан / бутан и хексан / 2,3-диметилпбутан.
Теоретични задачи
Задача Т1. Припомнете си работа с матрици в Excel от лекцията "Работа с матрици в програмата Excel".
Задача Т2. Решете системата (5) от две уравнения и две неизвестни така както е описано в текста по-горе и получете инкрементите hC-C и hC-H от данните за етан и пентан.
Задача Т3. От таблица 1 съставете друга система с две уравнения и две неизвестни, например от данните за метан и етан и решете системата от уравнения. Получават ли се подобни по големина инкременти?
Задача Т4. Напишете броят метилови, метиленови и метинови групи в съединенията 2-метилпентан и 3-метилпентан. Има ли разлика в техния брой? Но техните стандартни топлини на образуване са различни.
Практически задачи
Задача C1. Отворете файла "heats_form.xls" . Разгледайте четирите таблици (sheets), в които са проведени изчисленията. Копирайте данните за алканите в нов файл и се опитайте да повторите изчисленията.
[1] K. Varmuza; Chemometrics. Springer Verlag, Berlin, 1980.
[2] D.L. Massart, B.G.M. Vandeginste, S.N. Deming, Y. Michote, L. Kaufman; Chemometrics: A Textbook. Elsevier, Amsterdam, 1988.
[3] 4. В.А. Киреев; Методы практических расчетов в термодинамике химических реакции. Химия, Москва, 1975.
[4] James G. Speight; Lange’s Handbook
of Chemistry.Sixteenth Edition. McGraw-Hill, New York, 1980.
..
Автор: Пламен
Пенчев, Ph.D.
Авторски права: Материалът или част от него могат да се използват свободно (копирани на друг сайт) в обучението на български или македонски студенти само ако в сайта изрично се цитира тази оригинална статия във вида: П.Пенчев, Многопроменлив регресионен анализ, Списание "Коснос" (www.kosnos.com), брой 35, 2009 г.
[ това е статия от брой 35 от ноември 2009 г. на списание "Коснос" www.kosnos.com ]