С този материал започнахме една поредица за приложение на статистиката в химията. Материалът може да се използва не само от химици, а от всички, които се занимават с обработка на експериментални резултати.

Разпределението на Стюдънт е разпределение на случайна величина t_n = У/Х, където У е стандартно разпределена случайна величина, а Х e c2-разпределена случайна величина, със степени свобода, равни на n. Обикновено степените свобода се отбелязват с f. Плътността на t-разпределението се дава с уравнение (1):

        р(t) = Г[(n+1)/2]/[Sqrt(np) Г(n/2)](1 + t²/n)^(n+1)/2,                         (1)

където Sqrt() означава корен квадратен, а Г() е гама функцията.

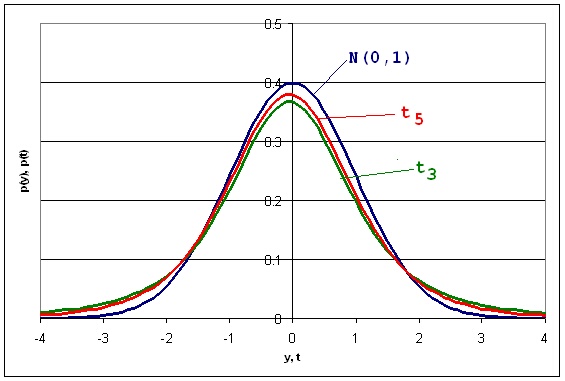
Плътността на t-разпределението е камбановидна крива, симетрична отностно правата t = 0, която е по-малко стръмна от тази на стандартното разпределение и при нарастване на степените свобода f клони към нея. На фигура 1 са дадени няколки криви на плътността на t_f-разпределението при различни f, както и плътността на стандартното разпределение.

Пример за t_N-1 разпределена величина е t_N-1 = (`Х - m)Sqrt(N)/S, където `Х е средната величина на N резултата, S е тяхното стандартно отклонение, а m  е математическото им очакване; резултатите Х_k са нормално разпределени. Забележете, че степените свобода са равни на броя измервания минус едно, f = N - 1.

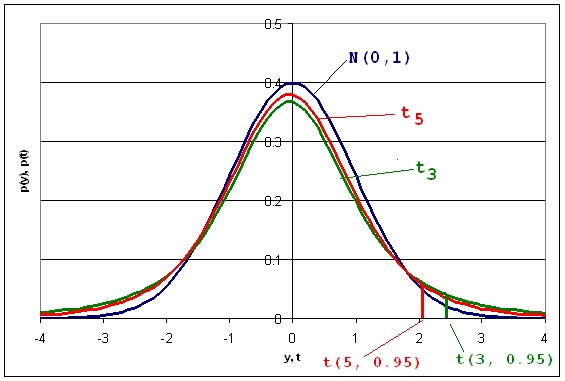
В приложение 3 са дадени интегралните граници t(f, P) на t-разпределението, т.е. решенията на F(t(f, P)) = P, за P равно на 0.50, 0.75, 0.90, 0.95, 0.98 и 0.99, както и F'(t(f, P')) = P', съответно за P' = 0.75, 0.875, 0.95, 0.975, 0.99 и 0.995. F(t) е функцията на t-разпределението, която е равна на интеграл от плътността в граници от -w   до t, а F'(t) = 2F(t) - 1 и е интеграл от плътността в граници от -t до t. За първото решение (F(Х) = число) се казва, че е при едностранна постановка на въпроса, а за второто (F'(Х) = число)  при двустранна постановка на въпроса. Тези интегрални граници зависят от степените свобода f, което ясно се вижда на фигура 2.

Пример 1. Да се намери вероятността t₉-разпределена случайна величина да заема стойности:

а) по-малки от 2.8

б) в интервала (2.8, 2.8)

Решение:

От приложение 3 се намира, за f = 9 и интегрална граница 2.82, че статистическата сигурност е 0.99 за едностранна постановка на въпроса и 0.98 за двустранна постановка, т.е. съответните вероятности са около 0.99 и 0.98 (Работи се с 2.82, което е близко по стойност до 2.80).

Пример 2. Проведени са десет измервания на олово в детски храни. Те са със средната стойност `Х = 2.81 мкг/мл и със станадартно отклонение S = 0.3 мкг/мл. Да се намери интервалът, за който `Х е среда и вероятността истинската стойност да е в него е 0.98.

Решение:

Величината t₉ = (`Х - m)Sqrt(10)/S е t₉ разпределена, със степени свобода f = 9. От приложение 3 се вижда, че за f = 9 и статистическа сигурност 0.98 при двустранна постановка на въпроса интегралната граница е 2.82 (вижте предишния пример!), т.е. вероятността t₉ разпределена величина да е в интервала (-2.82, 2.82) е 0.98. Приложено това към задачата дава

 Р(2.82 < (`Х - m) Sqrt(10)/S < 2,82) = 0.98, т.е. истинската стойност е с вероятност 0.98 в интервала

При заместване на конкретните стойности`Х  = 2.81 и S = 0.3 се получава, че съдържанието на олово е в интервала (2.54, 3.08) с вероятност 0.98.

Автор: Пламен Пенчев, Ph.D.