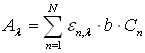 (5)
(5)
За пълноценно усвояване на настоящия материал е необходимо читателят да се запознае, не само с предноцитираната лекция, но и с лекцията "Работа с матрици в програмата Excel". Тъй като настоящият материал използва УВ-Вид спектри (т.н. Електронни спектри или спектри във видимата и ултравиолетовата област), то читателят може да се запознае със спектралните методи от лекциите по молекулна спектроскопия на проф. дхн Георги Андреев, които са публикувани в нашето списание - вижте линковете в частта литература в края на тази лекция.
1. Електронни спектри на смес от вещества. Обикновено UV/Vis спектър на едно вещество се измерва в региона от 200 до 900 nm. Ако I0 е интензитетът на пропуснатото през пробата лъчение, а I е интензитетът на преминалото през пробата лъчение, то величината А се нарича абсорбция и измерва степента на поглъщане на лъчението
А = lg (I / I0) (1)
С lg() е означен десетичен логаритъм.
За коя да е точка на спектъра се изпълнява закона на Буге-Лаберт-Беер за някакъв регион от концентрации на веществото, чийто спектър се измерва (вижте материала Закон за абсорбция на светлината)
A = a b c = e b C, (2)
където b е дебелината на слоя поглъщащо вещество и c е произволна концентрация, а C е молярна концентрация. Величината a се нарича абсорбируемост; ако дебелината на слоя, b, се измерва в cm, а концентрацията в mol/l, то тогава се изписва втората част на уравнение (2) и e представлява молярната абсорбируемост на веществото, която има мерни единици [l mol-1 cm-1].
Моларната абсорбируемост зависи от природата на веществото, температурата и от дължината на вълната, l. Последният факт често се отбелязва с по следния начин
Al = el b C, (3)
Ако имаме смес от няколко вещества, които не си взаимодействат химически и не образуват силни междумолекулни връзки (от типа на водородните връзки), то спектърът на тази смес, Al, е математическа сума от спектрите на отделните компоненти на сместта, ако последните спектри са измерени при концентрации на компонентите, Cn, равни на концентрациите им в сместта.
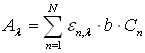 (5)
(5)
където сумата е по отделните компоненти на сместта, n, чийто брой е равен на N. Cn е концентрацията на n-тия компонент, а el,n е молярната абсорбируемост на n-тия компонент при дължина на вълната l.
Ако измерим UV/Vis спектри на поредица от разтвори, в които концентрациите на компонентите варират, то уравнение (5) може да бъде записано за всеки един от тях по следния начин:
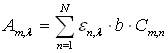 (6)
(6)
С индекси са означени размерностите на матриците, M, N и L, които съответно означават следното: M е броят разтвори, N – броят компоненти в разтворите, а L – броят дължини на вълните, при които става измерването на абсорбцията. Последната стойност се нарича по-общо брой на детекторите. Матрицата K се нарича матрица на чувствителностите и очевидно се дава с израза
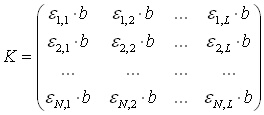 (8)
(8)
Елементът kn,l в нея представлява чувствителността за n-тия компонент при l-тата дължина на вълната. На практика това е наклонът, k, на калибрационната права A = k C, която може да се построи на тази l-та дължина на вълната, ако се измерват разтвори, съдържащи само n-тия компонент, без наличие на другите компоненти и други пречещи (т.е. поглъщащи лъчение на тази дължина на вълната) вещества. Обърнете внимание, че отрезът се предполага равен на нула; това обикновенно се постига в UV/Vis спекроскопия, ако се извърши корекция на базовата линия преди да се осъществят измерванията.
2. Многокомпонентен анализ на смеси от вещества. Ако рангът на матрицата CM,N от уравнение (7) e по-голям или равен на броят компоненти N, т.е. rang(CM,N) > N, то могат да се намерят без проблем елементите на матрицата на чувствителностите, К. Необходимо условие за това неравенство е броят на разтворите M да по-голям или равен на броят на компонентите, т.е. M > N. При изпълнение на последното условие предходното условие ще се изпълнява ако има поне N на брой разтвора, чийто концентрации представляват линейно независими вектори (с размерност N). Приготвянето на тези N разтвора е задача на експериментатора, която той трябва да планира внимателно: например за два компонента, два разтвора с концентрации на компонентите, съответно (1.0 x 10-4M, 2.0 x 10-4M) и (2.0 x 10-4M, 4.0 x 10-4M), представляват линейно зависими вектори (втория е два пъти по-концентриран от първия) и не могат да бъдат полезни при определяне на каквито и да е чувствителности на която и да е дължина на вълната по простата причина, че абсорбцията за втория разтвор на всяка дължина на вълната ще е два пъти по-голяма от тази на първия разтвор. Това лесно може да се провери математически по следния начин: уравнението на Буге-Ламберт-Беер за двата разтвора (всеки с два компонента) е следното
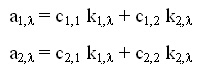 (9)
(9)
Тъй като концентрациите на компонентите във втория разтвор са двойни, т.е. c2,1 = c1,1 и c2,2 = c1,2 то
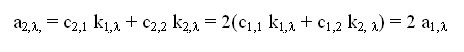 (10)
(10)
Това на практика означава, че това не са две уравнения с две неизвестни (k1,l и k2,l), а само едно уравнение, от което не могат да се намерят двете неизвестни.
Ако обаче разтворите са подготвени правилно то матрицата на чувствителностите може да се намери по следния начин, чрез последователно умножаване на двете страни на уравнение (7) отляво:
AM,L = CM,N KN,L
CTN,M AM,L = CTN,M CM,N KN,L
[CTN,M CM,N]-1 CTN,M AM,L = IN,N KN,L
или
KN,L = [CTN,M CM,N]-1 CTN,M AM,L
където IN,N е единична матрица с брой на редовете и колоните, равни на N.
Матрицата
[CTN,M CM,N]-1 CTN,M
се явявя своево рода обратна матрица на правоъгълната (в общия случай) матрица CM,N. Както споменахме в предишната точка тя се нарича обобщена обратна матрица и при квадратна матрица тя съвпада с обратната и матрица, стига последната да съществува. Една квадратна матрица има обратна, ако нейната детерминанта е различна от нула, т.е. нейният ранг е равен на размера и. А една правоъгълна матрица има обобщена обратна ако нейният ранг е равен на по-малката размерност, т.е. условията M > N и rang(CM,N) > N . Рангът няма как да е равен на по-голямата от двете размерности на матрицата, защото ранг на една матрица е размерността на най-голямата квадратна матрица, която може да се образува от нея, чрез зачеркване на редове и колони и която има детерминанта различна от нула!
След като се намери матрицата на чувствителностите концентрацията на поредица от неизвестни разтвори (S на брой), които са смес от същите компоненти, може да бъде намерена, ако те се измерят на същите дължини на вълните и чрез последователно умножаване на двете страни на уравнение (7) отдясно:. За тях ще е изпълнена зависимост, аналогична на уравнение (7); тяхната абсорбция и концентрация са отбелязани с прим, за да се различават от абсорбцията и концентрацията на стандартите.
A'S,L = C'S,N KN,L
A'S,LKTL,N = C'S,N KN,L KTL,N
A'S,LKTL,N[KN,L KTL,N]-1 = C'S,N [KN,L KTL,N][KN,L KTL,N]-1
или
C'S,N = A'S,LKTL,N[KN,L KTL,N]-1
където отново IN,N е единична матрица с брой на редовете и колоните, равни на N.
Матрицата
KTL,N[KN,L KTL,N]-1
се явявя своево рода обратна матрица на правоъгълната (в общия случай) матрица KN,L.
За да има матрицата [KN,L KTL,N]обратна матрица, то тя трябва да има детерминанта, различна от нула. А за да е изпълнено това и да могат горните равенства да се изпълнят, трябва rang(KN,L)> N. Необходимо условие за това е L > N, а достатъчно условие е дължините на вълните така да са избрани, че компонентите да абсорбират коренно различно лъчението на тях. Това последното е свързано с избягване на изосбестичните точки на двойките спектри - вижте тази статия за изосбестичните точки. На практика изследователят избира дължините на вълните и може да осигури изпълнението на това условие.
Теоретични задачи
Задача Т1. Припомнете си работа с матрици в Excel от лекцията "Работа с матрици в програмата Excel".
Задача Т2. Проверете, че при умноженията на матрици в уравнения (11) и (12) се спазва условието, че броя колони на лявата матрица са равни на броя редове на дясната матрица. А също така, че резултантната матрица има брой редове, равен на редовете на лявата матрица и брой колони, равен на броя колони на дясната матрица.
Практически задачи
Задача C1. Отворете Excel файла amacan.xls. Разгледайте таблицата (sheet) “MultiCompAnalysis”, в която са дадени пет стандартни разтвора от три аминокиселини (тирозин, фенилаланин и триптофан), както и три "неизвестни" проби, съдържащи същите компоненти. В клетки B2:D9 са дадени концентрациите на тези осем разтвора, а в клетки F2:N9 - техните УВ спектри (по-точно абсорбцията на избрани 9 дължини на вълните, дадени в първия ред в нанометри).
В същата работна таблица са извършени матричните операции, описани в уравнения (11) и (12). Опитайте се да свържите тези уравнения с действията, извършени в работната таблица. Обърнете внимание, че броят на стандартните разтвори е пет, M = 5, броят на компонентите е три, N = 3, броят на дължините на вълните (дететорите) е девет, L = 9, а броят на неизвестните разтвори е три, S = 3.
Задача C2. Във файла amacan.xls отворете таблицата (sheet) “WORK” и направете изчисленията по подобие на тези в таблица “MultiCompAnalysis”. Това са поредица от изчисления, които дават следните две зависимости
K3,9 = [CT3,5
C5,3]-1
CT3,5
A5,9
и
C'3,3 = A'3,9KT9,3[K3,9 KT9,3]-1
Задача C3. В таблицата “WORK” на файла amacan.xls намерете в клетки F19 и M32, съответно детерминантите на матриците [CT3,5 C5,3] и [K3,9 KT9,3]. Различни ли са от нула?
Задача C4. Създайте нова таблицата “Multi6” във файла amacan.xls. С мишката се отива на означението на таблицата “WORK” и се кликва с десния бутон на мишката. От локалното меню изберете Insert… и от появилия се прозорец изберете иконата Worksheet. Копирайте тази част от данните от таблица “WORK”, която отговаря на първите 6 дължини на вълните (това е правоъгълника A1:K9). Повторете изчисленията от задача C3. Внимавайте за размерността на матриците – някои от тях ще имат различна размерност.
[1] М. А. Шараф, Л. Иллмэн, Б.Р. Ковальски; Хемометрика. Химия, Ленинград, 1989.
[2] D.L. Massart, B.G.M. Vandeginste, S.N. Deming, Y. Michote, L. Kaufman; Chemometrics: A Textbook. Elsevier, Amsterdam, 1988.
[3] Г. Андреев. Молекулна спектроскопия, Изд. ПУ “П. Хилендарски”, Пловдив, 1999. По-голяма част от тези лекции са публикувани в нашето списание, вижте съдържанието. Ето връзки към пет от лекциите по УВ-Вид спектроскопия:
Автор: Пламен Пенчев, Ph.D.
Авторски права: Материалът или част от него могат да се използват свободно (копирани на друг сайт) в обучението на български или македонски студенти само ако в сайта изрично се цитира тази оригинална статия във вида: П.Пенчев, Многокомпонентен анализ на смеси, Списание "Коснос" (www.kosnos.com), брой 35, 2009 г.
[ това е статия от брой 35 от ноември-декември 2009 г. на списание "Коснос" www.kosnos.com ]